...
top: | | 4 | |
Wyznacz przedziały monotoniczności funkcji f(x)=x+ |
| |
| | x | |
Df=Df'=R\{0}
(x−2)(x+2)=0
i teraz mam problem z wykresem.. nie wiem czy dobrze go rysuje, zaznaczam −2 i 2
oraz 0 od którego zawsze odbijam tak jakby to co było wyłączone z dziedziny było parzystej
krotności − dobrze robię? Wówczas wychodzi f{rosnąca}=(−
∞;−2>u<2;
∞), f{malejaca}=<−2;2>\{0}
14 wrz 19:43
Janek191:
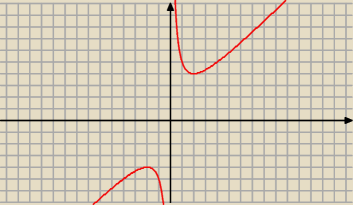
14 wrz 19:46
Janek191:
Nie można tak pisać .
Powinno być : f rośnie w przedziałach: ( − ∞; − 2) , ( 2 ; + ∞)
a maleje w : ( − 2 ; 0) , ( 0; 2)
14 wrz 19:48
top: dzięki za wykres, ale patrzyłem już na ten wygenerowany przez wolfram.
mam więcej zadań w których muszę uwzględniać dziedzinę i wyznaczać przedziały, więc
chciałbym wiedzieć czy ten sposób z odbijaniem od tego co jest wyłączone z dziedziny jest
poprawny, z gory dzieki

14 wrz 19:50
top: dodając post nie widziałem Twojej 2. odpowiedzi.
czyli, że sam zapis jest zły, ale sposób rozwiązywania dobry?
14 wrz 19:51
Janek191:
Można tak ująć

W ( − 2 ; 2) funkcja nie maleje, bo
f( − 1) < f(1)
14 wrz 19:55
top: no to wszystko jasne, dzięki bardzo
pytanie jeszcze trochę z innej beczki − wiesz może jak wolframem czy czymkolwiek innym
sprawdzać przedziały monotoniczności? rozwiązałem trochę takich zadań i chciałbymzobaczyć czy
są dobrze.
14 wrz 19:58
Janek191:
Poniżej jest funkcja : " rysuję "
Można rysować wykresy

14 wrz 20:10


 W ( − 2 ; 2) funkcja nie maleje, bo
f( − 1) < f(1)
W ( − 2 ; 2) funkcja nie maleje, bo
f( − 1) < f(1)
