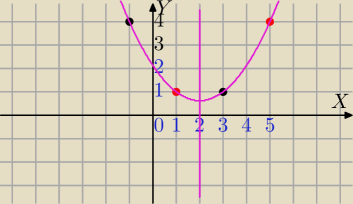
Równanie paraboli przechodzącej przez punkty nowy geniusz matematyki: Napisz równanie paraboli, która przechodzi przez punkty A=(1,1) i B=(5,4), a jej osią symetrii jest prosta x=2 . Przeszedł do klasy matematycznej i mam duże zaległości które staram się nadrobić. Doszedłem do momentu, gdzie obliczyłem a i b (nie jestem w 100 % czy to jest potrzebne ) i nie wiem co dalej robić

J: f(x) = ax² + bx + c f(1) = 1 f(5) = 4

	b
−		= 2
	2a

podstaw i oblicz: a, b, c

Mila: x_w=2 pierwsza wsp.wierzchołka paraboli

	−b
xw=
	2a

−b
	=2
2a

b=−4a f(1)=1 f(5)=4 f(3)=1 f(−1)=4 f(x)=ax²+bx+c f(x)=ax²−4ax+c f(1)=a−4a+c=1⇔−3a+c=1 f(5)=25a−20a+c=4⇔5a+c=4 Mamy układ: 5a+c=4 −3a+c=1 8a=3

	3
a=
	8

	3		3
b=−4*(		)=−
	8		2

	3		15		1
c=4−5*(		)=4−		=2
	8		8		8

	3		3		17
f(x)=		x2−		x+
	8		2		8