planimetria magda: W trójkącie ABC długości boków AC i BC są odpowiednio równe 2 i 4, zas miara kąta ACB wynosi 120 stopni. Oblicz dł. odcinka, który jest czescią wspólną dwusiecznej kąta ACB i trójkąta ABC. Bardzo proszę o pomoc..

magda: oblicz długosc tej czesci dwusiecznej kata ACB,która jest zawarta w trójącie ABC, takie jest polecenie

magda: jest ktos w stanie? wyliczylam trzeci bok z twierdzenia cosinusow i wyszedl 2√7,lecz nie rozumiem drugiej czesci zadania

magda: ?

Tadeusz: tylko po co Ci ten bok?

magda: nie wiem,bo nie rozumiem drugiej czesci zadania

magda: tzn, z tego wyliczę długość dwusiecznej

Tadeusz: ...pobaw się polem trójkąta i trójkątów

magda: chciaz nie,nie

Tadeusz: poradzisz? Jest prościutkie

Nuti:

	4
dwusieczna ma długość		− dowód z twierdzenia Talesa. Spróbuję zrobić rysunek...
	3

magda: z pol trojkatow jak powidzial Tadeusz dwusieczna wyszla mi 4

magda:

	4
pomylilam sie, jednak dwusieczna to		,racja
	3

Tadeusz:

magda: W trójkącie ABC z wierzchołka kąta prostego poprowadzono wysokość CD i środkową CE. Oblicz stosunek |CE| do |CD| ,jeśli wiadomo ,że przyprostokątne są w stosunku 1:2 / pomożecie ?

magda: oznaczylam przyprostokatna jedna jako x ,druga jako 2x i wyliczylam przeciwprostokatna,ktora wyniosla √3x i nie bardzo wiem co dalej

Tadeusz: 8sin120^o=2xsin60^o+4xsin60^o 8=6x ⇒ x=4/3

magda: Tadeusz,dalej mowisz o zadaniu,ktore podalam jako pierwsze z dwusieczną?

Tadeusz: tak ... w kontekścieTwego "zarzutu" z 19:19

magda: po 4 minutach poprawilam się

magda: bo zauwazylam blad. moze ktos pomoc z tym drugim zadaniem?

magda: ?

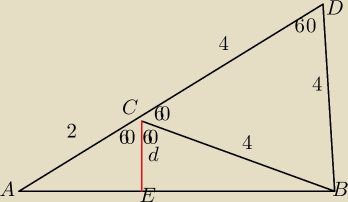
Nuti: Wracam do mojego rozwiązania pierwszego zadania, bo szkoda mi sposobu z Talesa W trójkącie ABC bok AC ma długość 2, bok BC ma długość 4, a kąt między nimi jest równy 120 stopni. CE jest dwusieczną kąta ACB. Mamy obliczyć jej długość (d). Przedłużamy bok AC o 4 i zaznaczamy punkt D. Kąt DCB ma 60 stopni, jako uzupełniający kąt ACB do 180. Stąd trójkąt CBD jest równoboczny i BD jest równoległe do CE (kąty!), zatem mamy z twierdzenia Talesa:

CE		AC
	=
BD		AD

czyli

d		2
	=
4		2+4

	4
czyli d=		.
	3

Nuti: @magda pomogę

magda: To zadanie napisalam,ze zrobilam , prosiłam o poomoc z drugim

magda: a co do drugeigo to te trzeci bok to √5 ,pomylka w obliczeniach.

Nuti:

	4
W drugim zadaniu wyszlo		.
	5

Nuti: Napisałam drugie rozwiązanie pierwszego, bo jest ładne, z Talesa.

Nuti: Napiszę ci rozwiązanie drugiego, ale to trochę potrwa, bo ja jestem strasznie powolna w rysowaniu.

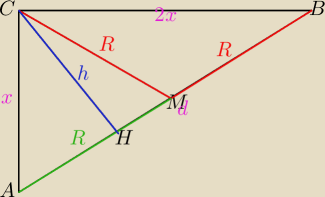
Nuti: 1. Skoro długość AC do długości CB jest jak 1 do 2, to można oznaczyć pierwszą z nich przez x, a druga będzie wówczas 2x. 2. W trójkącie prostokątnym środek przeciwprostokątnej jest środkiem okręgu opisanego na tym trójkącie (z twierdzenia o kątach wpisanym i środkowym opartych na tym samym łuku), stąd długości odcinków CM (środkowa), AM i BM są równe R (ten promień właśnie).

	4
3. Z twierdzenia Pitagorasa: x2+(2x)2=(2R)2, czyli x2=		R2.
	5

4. Liczymy pole trójkąta na dwa sposoby:

1		1		4
	*h*2R =		*x*2x = x2 =		R2
2		2		5

stąd

	4
h*R =		R2
	5

więc

h		4
	=
R		5

	4
Stosunek długości wysokości do długości środkowej jest		.
	5

Nuti: Różowe „d" na rysunku to jakiś śmieć.

Nuti: Pomyłkowo użyłam M (od „mediana") zamiast E i H (spodek wysokości) zamiast D. Stary zwaczaj...