środkowe w trojkacie, pole. trororror: Dane jest pole trójkąta ABC=S. Oblicz pole trójkąta, którego bokami są środkowe danego trójkąta.

Kacper: Ciekaw jestem jak narysujesz ten trójkąt

Nuti: Interesujące... Na pewno się nie pomyliłeś przy przepisywaniu treści? @Kacper Nie trzeba go koniecznie rysować, może da się wyliczyć. Ale zadanie jest intrygujące, muszę spróbować. Klasyczne jest oczywiście zadanie dotyczące trójkąta o wierzchołkach w środkach boków danego trójkąta, ale ono jest super łatwe. To jest ciekawe.

Nuti: Może uda się coś odgadnąć na podstawie szczególnego przypadku.

	a2√3
Weźmy trójkąt równoboczny o boku a, pole to		, środkowe są jednocześnie
	4

	a√3
wysokościami, ich długości to		, tworzą więc trójkąt równoboczny o polu
	2

	3		a2√3		3
		*		, czyli stosunek pól jest		.
	4		4		4

Może to jest ogólna zasada dla dowolnego trójkąta? Mamy w każdym razie hipotezę

Nuti: Wydaje mi się, że mam rozwiązanie, z symetrii środkowej. Pomęczę się nad rysunkiem − w międzyczasie na pewno ktoś szybszy zaprezentuje rozwiązanie

Mila: Narysować dowolny Δ i jego środkowe.

	3
SΔs=		S
	4

Nuti: '

Nuti: @Mila Nie rozumiem, co to da i jak doszłaś do rozwiązania.

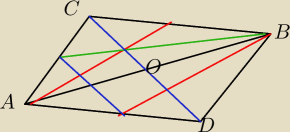
Nuti: Dany trójkąt ABC (na rysunku) i jego środkowe. Przekształcamy ten trójkąt w symetrii środkowej wobec środka O boku AB. Otrzymujemy równoległobok. Środkowa (czerwona) w trójkącie ABD jest obrazem w tej symetrii środkowej wychodzącej z wierzchołka A w trójkącie ABC, stąd równoległość i ten sam kolor. Z twierdzenia Talesa krótki niebieski odcinek łączący środki AC i AD jest równoległy do środkowej CO i ma taką samą długość jak ona. Trójkolorowy trójkąt na rysunku jest więc trójkątem zbudowanym ze środkowych trójkąta ABC. Wystarczy policzyć stosunek jego pola do pola tr. ABC (albo całego równoległoboku, który ma pole 2 razy większe niż pole tr. ABC). Teraz to już pewnie z górki, ale najpierw to wyślę.

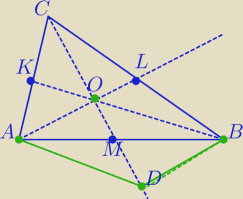
Mila: P_ABC=S S'− pole Δ zbudowanego ze środkowych.

	1
Przedłużam środkową CM w taki sposób, że |OM|=|DM|=		|CM|
	3

Czworokąt ADBO jest równoległobokiem, ( przekątne dzielą się na połowy) zatem:

	2
|DB|=		|AL|
	3

	2
ΔBOD∼Δ zbudowanego ze środkowych w skali k=		⇔
	3

PΔBOD		2
	=(		)2
S'		3

	1
PΔDBM=POMB=		S
	6

	1		1
PΔBOD=2*		S=		S
	6		3

1   S 3		4
	=		⇔
S'		9

	3
S'=		S
	4

=========

Nuti:

	3
Jasne, będzie		:
	4

Pole równoległoboku to 2S (S − pole trójkąta ABC), ale jednocześnie to h*AB=h*CB, gdzie h jest odległością między CB a AB, czyli wysokością równoległoboku. Pole trójkąta utworzonego ze środkowych (trójkolorowy na rysunku) to pole równoległoboku minus pola trzech trójkątów. Niestety, brakuje mi oznaczeń na rysunku, a nie mogę do niego wrócić, więc wyjaśnię, że będę po kolei odejmowała pole trójkątów: 1. CB(środek AC) 2. BD(środek AD) 3. A(środek AC)(środek AD). Pole tójkąta ze środkowych jest więc równe:

	1		1		1		1		1		1		1
2S −		*		h*CB −		*h*		AD −		*		h*		AD=
	2		2		2		2		2		2		2

	1		1		1		3
= 2S −		S −		S −		S=		S.
	2		2		4		4

Nuti: @Mila Z czego wynika, że pole trójkąta OMB jest szóstą częścią pola całego trójkąta? Nie widzę tego, a ty tego nie uzasadniasz.

Nuti: Sorry, forget it!

Mila:

PW: Nie chcę być złośliwym chochlikiem, ale skąd pewność, że istnieje twór, którego pole liczymy? − czy zawsze ze środkowych trójkąta można utworzyć trójkąt? Taka mała zagwozdka.

Mila: Do PW Zawsze.

	2		2		2
Skoro zbudowałam Δ o bokach		s1,		s2,		s3
	3		3		3

to mogę też zbudować Δ o bokach s₁,s₂,s₃. Powinnam to napisać w odpowiednim miejscu rozwiązania. Autorka nie jest zainteresowana.

Mila: Uwaga była słuszna.

PW: