wykres
Metis: Jak szybko wyznaczyć zbiór wartości funkcji:
13 wrz 19:34
Kacper:
W pamięci

13 wrz 19:37
Metis: No tak, ale nie wiem jak to poprawnie zapisać

A jak napiszę bez jakiegokolwiek uzasadnienia nie zostanie zaliczone

13 wrz 19:40
Metis: A jeśli *
13 wrz 19:40
Kacper:
−1≤sin2x≤1
Niech sin2x=t i −1≤t≤1
| | 2 | |
Teraz rysujesz funkcję f(t)= |
| , t≠0 i odczytujesz jej zbiór wartości w podanym przedziale |
| | t | |
dla t

Odp. Zw
f=(−
∞,−2>∪<2,+
∞)
13 wrz 19:44
13 wrz 19:45
Metis: No dobra, zaraz to ogarnę

| | 1 | | 2 | | √3 | |
Powiedzcie mi jeszcze czy | |
| |< |
| ⇔ |sin2x|< |
| |
| | sin2x | | √3 | | 2 | |
13 wrz 19:48
Kacper:
Benny nie za szybko?

13 wrz 19:48
ICSP: nie
13 wrz 19:49
Metis: | | 2 | |
−2≤ |
| ≤2  |
| | sin2x | |
13 wrz 19:49
Benny: Tak zabrakło tam 2.
Coś nie tak
Kacper?

13 wrz 19:50
Metis: Nierówności w złą stronę

13 wrz 19:51
henrys: @benny nie zapisałeś poprawnie, z Twojego zapisu wynika, że −1≥1
13 wrz 19:52
Metis: | | 1 | | 2 | | √3 | |
Ale | |
| |< |
| ⇔ |sin2x|> |
| ? |
| | sin2x | | √3 | | 2 | |
13 wrz 19:53
ICSP: nadal nie
13 wrz 19:53
Benny: Teraz widzę.
Metis u Ciebie teraz będzie, że y∊<−2;2>
13 wrz 19:54
Kacper:
Benny niestety, ale zbiór wartości jest inny

13 wrz 19:55
Metis: Dziwne

Mam własnie takie przejście w zeszycie i nie wiem skąd się wzięło.
| | 1 | | 2 | | √3 | |
| |
| |< |
| ⇔ |sin2x|> |
| |
| | sin2x | | √3 | | 2 | |
13 wrz 19:57
Benny: No zbiór będzie y∊(−
∞;−2>∪<2;+
∞)

13 wrz 19:58
Metis: Oczywiscie dziedzinę pomijam.
13 wrz 19:59
Kacper:
Możesz pomnożyć nierówność
| | 1 | | 2 | |
| |
| |< |
| , sin2x≠0 |
| | sin2x | | √3 | |
przez |sin2x|, bo |sin2x|>0
i wtedy masz kolejno:
| | 2 | | 2 | |
1< |
| |sin2x| (dzielimy przez |
| ) |
| | √3 | | √3 | |
13 wrz 20:01
Metis: Hmmm ja też źle zapisałem ten przedział:
13 wrz 20:06
Metis: Wyznaczę ten zbiór wartości tak jak ty proponujesz
Kacper 
13 wrz 20:14
Benny: Myślę, że moje rozwiązanie jest dobre tylko nie należy go zapisywać w podwójnej nierówności.
13 wrz 20:16
Metis: Dziękuje Wam !

13 wrz 20:23
PW: | | π | | π | |
Znamy własności funkcji sin2x − jest rosnąca na przedziale [− |
| , |
| ], który ma |
| | 2 | | 2 | |
długość okresu. Wystarczy więc wyznaczyć jej zbiór wartości na tym przedziale. Funkcja
nie jest określona dla x = 0, wobec tego liczymy granice przy x→0
− i przy x→0+, a na
pozostałych krańcach zbioru określoności podstawiamy:
| | 2 | | 2 | |
|
| = −2, |
| = 2. |
| | sin(−π) | | sinπ | |
13 wrz 22:58
Mila:
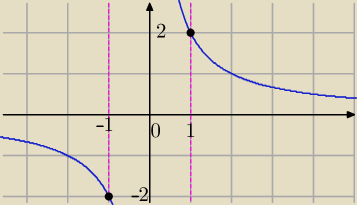
|t|≤1
13 wrz 23:02
13 wrz 23:06
pigor: ..., warto zauważyć, że
| | 2 | | 2*1 | |
f(x)= |
| = |
| = U{2(sin2x+cos2x)}= ...= tgx+ctgx, teraz |
| | sin2x | | 2sin2xcosx | |
"sumując wykresy" funkcji y=tgx i y=ctgx :
Z.W.= (−∞;−2) U (2;+∞). ...

14 wrz 02:08
pigor: ..., oczywiście w mianowniku ma być 2sinxcosx. ...

14 wrz 02:09
pigor: ... , no i dalej wiadomo...; idę spać

14 wrz 02:19

 A jak napiszę bez jakiegokolwiek uzasadnienia nie zostanie zaliczone
A jak napiszę bez jakiegokolwiek uzasadnienia nie zostanie zaliczone
 Odp. Zwf=(−∞,−2>∪<2,+∞)
Odp. Zwf=(−∞,−2>∪<2,+∞)






 Mam własnie takie przejście w zeszycie i nie wiem skąd się wzięło.
Mam własnie takie przejście w zeszycie i nie wiem skąd się wzięło.



 |t|≤1
|t|≤1


