geometria analityczna
Wariorreaktywacja: napisz równanie okręgu stycznego do prostej 5x−12y−24=0 , którego środkiem jest punkt
przecięcia prostych 8x−3y−27=0 i 3x+2y−32=0
13 wrz 18:22
Wariorreaktywacja: Pomoże ktoś to rozwiązać , lub naprowadzić mnie i podpowiedzieć od czego zacząć , choć ja dobry
byłem z matmy , jednak 2 tygodnie choroby robi swoje


13 wrz 19:05
Tadeusz:
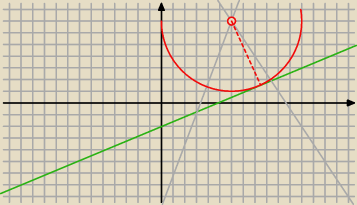
13 wrz 19:12
Eta:
| | ⎧ | 8x−3y−27 | |
| 1/ rozwiąż układ równań | ⎩ | 3x+2y−32=0 |
|
otrzymasz współrzędne punktu S(6,7)
2/długość promienia tego okręgu jest równa odległości punktu S od stycznej
S(6,7) s: 5x−12y−24=0
ze wzoru
| | |6*5+7*(−12)−24| | |
r=d= |
| =............ = 6 |
| | √52+122 | |
o: (x−x
S)
2+(y−y
S)
2=r
2
odp:
o: (x−6)2+(y−7)2=36
13 wrz 19:19


