Pola figur huragan: Pole trapezu ABCD jest równe 100 cm² , a krótsza podstawa DC tego trapezu ma 2 cm długości. Kąty ostre trapezu przy dłuższej podstawie AB oznaczamy przez α i β.

	4		8
Wiedząc że sinα =		, a tgβ =		, oblicz:
	5		15

a) obwód trapezu b) długość przekątnych tego trapezu

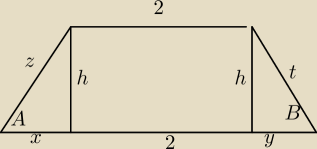
Nuti: Trochę tu dużo pisaniny, ale rozwiązanie jest proste. Trzeba tylko znać:

	1
1. wzór na pole trapezu P=		*h*(a+b), gdzie h jest wysokością, a a i b są długościami
	2

podstaw. Powiedzmy, że ta krótsza ma długość a, czyli a=2. Trzeba znaleźć b i h. Na moim niezręcznym rysunku b=x+2+y. 2. wzory na sinus i tangens oraz twierdzenie Pitagorasa. Muszę znaleźć x, y i h. Wtedy tylko podstawię do wzoru na pole, które jest równe 100, i wyliczę resztę. Na rysunku napisałam A zamiast α i B zamiast β, bo nie chciało mi się eksperymentować z greckimi literami w edytorze do rysunków.

	8		h		15
tgβ=		=		, czyli y=		h.
	15		y		8

	4		h		5
sinα =		=		, czyli z=		h.
	5		z		4

Dalej, z twierdzenia Pitagorasa x²+h²=z²

	5
Wstawiamy z=		h i mamy
	4

	25
x2+h2=		h2,
	16

czyli

	9		3
x2=		h2 i, jako że to wszystko dodatnie: x=		h.
	16		4

Wyślę to teraz i zaraz zrobię resztę, bo już nie widzę co robię (okienko zbyt małe...) cdn

Nuti: Wstawiamy teraz to wszystko do wzoru na pole, żeby wyliczyć h:

	1		3		15
100=		*h*(2+		h+2+		h)
	2		4		8

stąd wyliczamy h:

	21
200=h(4+		h)
	8

czyli 21h²+32h−1600=0. Nie, nie będę tego liczyć... Może się pomyliłam? W każdym razie po wyliczeniu h otrzymujemy x, y i z z wzorów w poprzednim poście, a t obliczamy z prawego trójkąta (też tw. Pitagorasa). Obwód to 4+x+y+z+t. Powodzenia! b) przekątne z twierdzenia Pitagorasa dla odpowiednich trójkątów. Wszystkie długości już masz, tylko podstawić i liczyć!

Nuti: Ha! W tym równaniu Δ to 135424, a pierwiastek z niej jest całkowity i równy 368. Będzie dobrze!

Nuti: h jest równe 8.

Nuti: x=6, y=15, z=10

Nuti: t²=h²+y²=289=17² t=17 Obwód = 4+6+15+10+17=52. Jak widać, proporcje w moim rysunku są bardzo mocno chybione Przekątne oblicz sobie sama, tylko Pitagoras. Powodzenia!

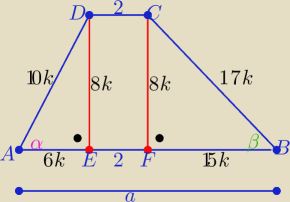
Eta: Dane zgodne z treścią zadania umieściłam na rysunku k>0 , b=2 a= 21k+2 h=8k P=100 to P=(21k+4)*4k=100 ⇒ 21k²+4k−25=0 ,Δ=2116, √Δ=46

	−4+46
k=		= 1 lub k= ...<0 −−odrzucamy
	42

zatem obwód trapezu: L= 4+48k=52 [j] Dla Nuti

Nuti: @Eta skąd wiedziałaś od początku, co jest wspólnym faktorem (k)? To było widać dopiero od pewnego momentu, prawda? To jeszcze nie wynikało z samej treści zadania? Czy przeoczyłam coś oczywistego? (Poza tym, że niepotrzebnie liczyłam równanie kwadratowe ze zbyt wielkimi współczynnikami.) Ale początkowe rozumowanie z trygonometrią i Pitagorasem trzeba było przeprowadzić, prawda?

Eta: Zgodnie z treścią zadania:

	8		8k		4		8		8k
tgβ=		=		, k>0 i sinα=		=		=
	15		15k		5		10		10k

h=8k itd...........

Nuti: Jasne. A za co się dostaje jabłko?

Eta: za "trud" w dłuuuugim .... rozwiązaniu

Nuti: no tak, trzeba podreperować nadwątlone siły...