zastosoanie rownan i nierownosci wykladniczych Dejwid: Witam, proszę o pomoc, rozbilem sobie z definicji wartosci bezwzglegnej i prubuje cos wzorami viet'a ale nic z tego dla mnie nie wynikaWyznacz wszystkie wartości parametru m (m ∈ R),

	1
dla których równanie |x2 + 4x| =		m − 3 ma dwa rozwiązania ujemne.
	2

Nuti: napisz słownie prawą stronę, bo nie wiem, czy to mnożenie czy potęgowanie i czy przypadkiem gdzieś nie zapomniałeś o nawiasie...

PW: Co by tam nie było po prawej stronie − oznacz to symbolem k i odpowiedz na pytanie: − Dla jakich wartości parametru k równanie |x² + 4x| = k ma dwa rozwiązania ujemne. Odpowiedź jest dość trudna, bo otrzymasz 2 równania kwadratowe ma dwóch podzbiorach zbioru liczb rzeczywistych. Formalnie obliczone x₁ i x₂ nie muszą być rozwiązaniami tych równań.

Kacper: Najprościej graficznie

Dejwid: jedna druga do potęgi m−3

henrys: 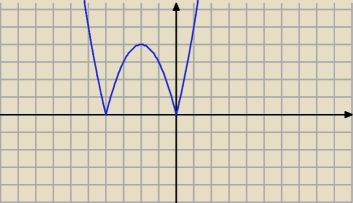|x²+4x|=k≠0 dla 0<k<4 trzy rozwiązania ujemne i jedno dodatnie dla k=4 mamy dwa rozwiązania ujemne i jedno dodatnie

	1
0<(		)m−3≤4
	2

Dejwid: a czy tego nie mozna rozwiazac algebraicznie?

J: można, rozbijasz na dwa równania kwadratowe z parametrem m i nakładasz odpowiednie warunki

Dejwid: mogłby ktos mi to pokazać?

J:

	1		1
x2 + 4x =		m − 3 lub x2 + 4x = −		m + 3
	2		2

warunki: Δ > 0 x₁ + x₂ < 0 x₁*x₂ > 0

PW: Dejwidzie, o 15:00 napisałem jak to zrobić. x² + 4x = x(x+4) jest liczbą nieujemną dla x∊(−∞,0]∪4,∞). Dla takich x mamy więc do czynienia z równaniem (1) x² + 4x = k, x∊(−∞,0]∪4,∞). Dla pozostałych x mamy równanie (2) − x² − 4x = k, x∊(0, 4). trudność polega na tym, że sama Δ i obliczenie pierwiastków nie wystarcza. Może być tak, że jedno z tych równań ma dwa pierwiastki ujemne, a drugie nie ma wcale, albo oba mają po jednym dodatnim i po jednym ujemnym, albo ... Koledzy dobrze podpowiadają: narysować jak henrys i sformułować zagadnienie tak: − Dla jakich m wykres funkcji wykładniczej przechodzi przez jeden punkt wykresu po "ujemnej stronie iksów" i przez wierzchołek. Przez "dziobek" w punkcie (−4, 0) przechodzić nie może, bo wykładnicza nie przyjmuje wartości 0, więc jest to jedyna możliwość. Podeprzeć rozumowanie wykresami kilku różnych funkcji wykładniczych na tym samym rysunku. Wystarczy chyba zbadać, dla jakich m funkcja wykładnicza podana po prawej stronie równania przechodzi przez wierzchołek kawałka paraboli i ile wtedy jeszcze ma punktów wspólnych z tymi kawałkami leżącymi po ujemnej stronie iksów (w drugiej ćwiartce).