wartość bezwzględna
mateusz: dlaczego podczas rozwiązywania nierówności np.
|x+2| < 3 podczas zastępowania układem nierówności jest "i"
a w np. |x+2| > 3 jest "lub"?
prosze o jak najprostsze wytłumaczenie

13 wrz 14:04
J:

zielony ... pierwszy przypadek
czerwony ... drugi
13 wrz 14:07
mateusz: nie do końca rozumiem

13 wrz 14:11
J:
IaI < A ⇔ −A < a < A
IaI > A ⇔ a > A lub a < −A
13 wrz 14:13
Aga1.: np. tak
1)
Ix+2I<3 ,nierówność < przekręć lekko w prawo , uzyskasz ⋀ (i)
2)
Ix+2I>3 , nierówność > przekręć lekko w prawo , uzyskasz ⋁ (lub
13 wrz 14:18
henrys:

Chyba najlepiej obrazuje tą sytuację interpretacja geometryczna wartości bezwzględnej.
|x+2| < 3
rozwiązaniem są takie liczby x, które są oddalone od −2 o mniej niż 3. Widzimy, że jest to
część wspólna x+2<3 i x+2>−3
Podaj interpretację geometryczną |x+2|>3, zastanów się czy zbiór rozwiązań tej nierówności
jest sumą czy iloczynem przedziałów?
13 wrz 14:19
J:
dobre...

13 wrz 14:19
mateusz : Sumą, ponieważ nie ma części wspólnych

Ale dalej nie wiem czemu w jednym przypadku używa się "i" a w drugim "lub"

13 wrz 14:41
J:
popatrz 14:13 ... pierwsza nierówność : i , a druga: lub
13 wrz 14:44
J:

a jest mniejsze od: A
i jednocześnie większe od : − A
13 wrz 14:46
J:

a jest mniejsze od − A
lub większe od A
13 wrz 14:48
henrys: Część wspólna oznacza przynależność do jednego i drugiego zbioru.
Suma zbiorów, przynależność do jednego lub drugiego (x jednocześnie nie może należeć do
jednego i drugiego zbioru)
13 wrz 15:04
PW: Im dłużej tłumaczymy, tym bardziej niezrozumiałe.
henrys już napisał nieprawdę

w tym
zapędzie (nieprawdę w sensie ogólnym, nie w odniesieniu do tego przykładu).
13 wrz 15:07
henrys: tak, tak w tym przypadku,
przecież nie będę pisał czym jest koniunkcja czy alternatywa
13 wrz 15:11
PW: Tak patrząc od początku świata (od definicji wartości bezwzględnej), to należy stwierdzić, że
w obu wypadkach jest to alternatywa.
Spokojnie, nie strzelać.
(1) |u| > 3
− co to znaczy? Ano, że (zgodnie z definicją wartości bezwzględnej)
u < 0 i −u > 3 lub u ≥ 0 i u > 3
u < 0 i u < −3 lub u ≥ 0 i u > 3
u < − 3 lub u > 3.
Alternatywa, oczywiste. Rozwiązanie jest sumą dwóch rozłącznych przedziałów:
u∊(−∞,−3)∪(3,∞).
(2) |u| < 3
− co to znaczy? Ano, że (zgodnie z definicją wartości bezwzględnej)
u < 0 i −u < 3 lub u ≥ 0 i u < 3
u < 0 i u > −3 lub u ≥ 0 i u < 3.
u∊(−3, 0) lub u∊[0, 3).
Alternatywa, oczywiste. Rozwiązanie jest sumą dwóch rozłącznych przedziałów:
(3) u∊(−3, 0)∪[0, 3).
Na tym można skończyć, ale przecież ostatnie rozwiązanie można zapisać w postaci "sklejonej":
u∊(−3, 3)
i sformułować to w postaci równoważnej obserwacji:
(4) |u| < 3 ⇔ −3 < u < 3.
Nie jest to jednak jakaś "nowa definicja" czy "prawda objawiona" do nauczenia − że jak ">" to
"lub", a jak "<" to "i" − to po prostu (3) daje się zapisać w prostszej postaci, co daje (4).
13 wrz 15:54
henrys: w tym wypadku koniunkcję możesz rozbić na alternatywę dwóch koniunkcji....
13 wrz 16:08
Aga1.: Dla kogoś kto jest na bakier z matematyką te wywody mogą zniechęcić całkowicie.
13 wrz 16:12
Mila:
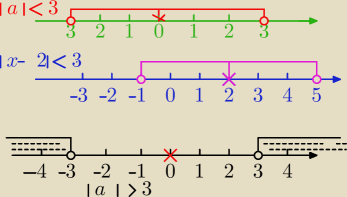
Zapis:
1) |a|<3 możesz interpretować, że chodzi o wszystkie liczby , których odległość od liczby 0
na osi liczbowej jest mniejsza niż trzy jednostki.⇔
−3<a<3 co możesz zapisać a>−3 i a<3
2)|x−2|<3 możesz interpretować, że chodzi o wszystkie liczby (x−2), których odległość od
liczby 0
na osi liczbowej jest mniejsza niż trzy jednostki.⇔
Stąd nierówność:
|x−2|<3 rozpiszesz tak:
x−2>−3 i x−2<3⇔
−1<x<5
==============
3)|a|>3⇔szukasz wszystkich liczb, których odległość od liczby 0
na osi liczbowej jest większa niż trzy jednostki.⇔
x<−3 lub x>3
Zatem nierówność:
|x−2|>3 rozpiszesz tak
x−2<−3 lub x−2>3
13 wrz 16:29
5-latek: Dzien dobry
Milu 
Pozdrawiam
Mateusz pyta się dlaczego ?
To ja się pytam Mateusza
dlaczego nie zajrzales do książki ?
13 wrz 16:37
mateusz: Dzień dobry 5−latku

Niestety nie mam tego w książce, ponieważ nie ma tego w podstawie do gimnazjum

dziękuje za odpowiedzi, już rozumiem


13 wrz 16:43
PW: Aga, ja się zabiję. Zniechęcić? Do czego? Do stosowania definicji wartości bezwzględnej?
Proponujesz w zamian "przekręcanie nierówności zgodnie z ruchem wskazówek zegara"? To jest
"mnemotechnika", a nie odpowiedź na pytanie "dlaczego".
13 wrz 16:44
Pawcio: Mila:
2)|x−2|<3 możesz interpretować, że chodzi o wszystkie liczby (x−2), """"których odległość od
liczby 0 na osi liczbowej jest mniejsza niż trzy jednostki""""
nie powinno być przypadkiem "odległość od liczby 2.." ?
13 wrz 18:23
Mila:
1) |x−2|<3
a=x−2
|a|<3 czyli chodzi o odległość liczb a od zera. ( za a jest podstawione x−2, czyli x
pomniejszone o 2)
Jeżeli chodzi o x , to odległość od liczby 2 jest mniejsza niż 3 jednostki.
2) |x−3|<5
odległość wszystkich x od liczby 3 jest mniejsza od 5.
Takie nierówności możesz graficznie rozwiązać, co przydaje się na maturze, bo masz zaznaczone
przedziały
na osi liczbowej i masz wybrać odpowiednią nierówność.
Albo masz podaną nierówność i trzeba wybrać ilustrację na osi.
13 wrz 21:42

 zielony ... pierwszy przypadek
czerwony ... drugi
zielony ... pierwszy przypadek
czerwony ... drugi

 Chyba najlepiej obrazuje tą sytuację interpretacja geometryczna wartości bezwzględnej.
|x+2| < 3
rozwiązaniem są takie liczby x, które są oddalone od −2 o mniej niż 3. Widzimy, że jest to
część wspólna x+2<3 i x+2>−3
Podaj interpretację geometryczną |x+2|>3, zastanów się czy zbiór rozwiązań tej nierówności
jest sumą czy iloczynem przedziałów?
Chyba najlepiej obrazuje tą sytuację interpretacja geometryczna wartości bezwzględnej.
|x+2| < 3
rozwiązaniem są takie liczby x, które są oddalone od −2 o mniej niż 3. Widzimy, że jest to
część wspólna x+2<3 i x+2>−3
Podaj interpretację geometryczną |x+2|>3, zastanów się czy zbiór rozwiązań tej nierówności
jest sumą czy iloczynem przedziałów?

 Ale dalej nie wiem czemu w jednym przypadku używa się "i" a w drugim "lub"
Ale dalej nie wiem czemu w jednym przypadku używa się "i" a w drugim "lub" 
 a jest mniejsze od: A i jednocześnie większe od : − A
a jest mniejsze od: A i jednocześnie większe od : − A
 a jest mniejsze od − A lub większe od A
a jest mniejsze od − A lub większe od A
 w tym
zapędzie (nieprawdę w sensie ogólnym, nie w odniesieniu do tego przykładu).
w tym
zapędzie (nieprawdę w sensie ogólnym, nie w odniesieniu do tego przykładu).
 Zapis:
1) |a|<3 możesz interpretować, że chodzi o wszystkie liczby , których odległość od liczby 0
na osi liczbowej jest mniejsza niż trzy jednostki.⇔
−3<a<3 co możesz zapisać a>−3 i a<3
2)|x−2|<3 możesz interpretować, że chodzi o wszystkie liczby (x−2), których odległość od
liczby 0
na osi liczbowej jest mniejsza niż trzy jednostki.⇔
Stąd nierówność:
|x−2|<3 rozpiszesz tak:
x−2>−3 i x−2<3⇔
−1<x<5
==============
3)|a|>3⇔szukasz wszystkich liczb, których odległość od liczby 0
na osi liczbowej jest większa niż trzy jednostki.⇔
x<−3 lub x>3
Zatem nierówność:
|x−2|>3 rozpiszesz tak
x−2<−3 lub x−2>3
Zapis:
1) |a|<3 możesz interpretować, że chodzi o wszystkie liczby , których odległość od liczby 0
na osi liczbowej jest mniejsza niż trzy jednostki.⇔
−3<a<3 co możesz zapisać a>−3 i a<3
2)|x−2|<3 możesz interpretować, że chodzi o wszystkie liczby (x−2), których odległość od
liczby 0
na osi liczbowej jest mniejsza niż trzy jednostki.⇔
Stąd nierówność:
|x−2|<3 rozpiszesz tak:
x−2>−3 i x−2<3⇔
−1<x<5
==============
3)|a|>3⇔szukasz wszystkich liczb, których odległość od liczby 0
na osi liczbowej jest większa niż trzy jednostki.⇔
x<−3 lub x>3
Zatem nierówność:
|x−2|>3 rozpiszesz tak
x−2<−3 lub x−2>3
 Pozdrawiam
Mateusz pyta się dlaczego ?
To ja się pytam Mateusza dlaczego nie zajrzales do książki ?
Pozdrawiam
Mateusz pyta się dlaczego ?
To ja się pytam Mateusza dlaczego nie zajrzales do książki ?
 Niestety nie mam tego w książce, ponieważ nie ma tego w podstawie do gimnazjum
Niestety nie mam tego w książce, ponieważ nie ma tego w podstawie do gimnazjum  dziękuje za odpowiedzi, już rozumiem
dziękuje za odpowiedzi, już rozumiem 
