Dla jakiego parametru m dziedziną jest R Ania: Mam problem z tym zadaniem: Dana jest funkcja f(x)= √(m−2)x²+(m−2)x+1 Dla jakich wartości parametru m jej dziedziną jest zbiór liczb rzeczywistych? Będę bardzo wdzięczna za pomoc i wyjaśnienia.

J: Warunek: (m−2)x² + (m−2)x + 1 ≥ 0 Rozpatrujesz trzy przypadki: 1) m = 0 2) m − 2 >0 3) m − 2 < 0

wmboczek: funkcja pod pierwiastkiem g(x)≥0 dla dowolnego x m−2>0 Δ≤0

J: @wmboczek ... a dlaczego m − 2 nie może być ujemne lub równwe 0 ?

PW: J po prostu pomylił zapis (ale nie rozumowanie, sądząc z kontekstu), powinno być 1) m − 2 = 0

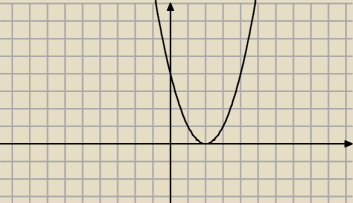
Aga1.: a>0 i Δ≥0 Oddzielnie sprawdzasz dla a=0, czyli m=2

J: oczywiście,że miało być: 1) m − 2 = 0

Kacper: Aga Δ≥0? coś nie tak

J: @Aga1 ... to samo pytanie .. a dlaczego nie moze być: m − 2 < 0 ?

Kacper: J oczywiście, że nie może myć m−2<0

Kacper: *być

J: faktycznie ... nie wiem coś mnie zaćmiło ... przepraszam

Aga1.: Dla jakiego m rozwiązaniem nierówności (m−2)x²+(m−2)x+1≥0 jest zbiór R? Nie mam racji?

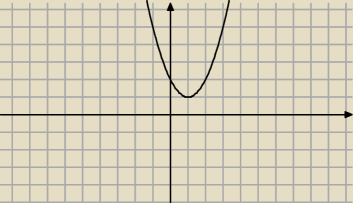
Aga1.: Oczywiście w pierwszym warunku powinno być m−2>0 i Δ≤0

Ania: A jakie jest założenie dla delty w 3) przypadku? Δ ≥ 0?

J: nie ma trzeciego przypadku..to była moja pomyłka

Aga1.: Ania o 13:55 wkradł mi się błąd, zamiast Δ≥0 powinno byćΔ≤0

Ania: Dlatego że wtedy działanie pod pierwiastkiem byłoby ujemne?

Ania: Dlatego nie ma 3 przypadku?

Kacper: Są tylko dwa przypadki: 1^o, kiedy nie mamy do czynienia z funkcją kwadratową, czyli m−2=0 2^o, gdy mówimy o funkcji kwadratowej m−2>0 i Δ≤0

Aga1.: Tak.

J: jeśli: m − 2 < 0, to funkcja pod pierwiastkiem nigdy nie będzie nieujemna dla każdego x ∊ R

Ania: Dobra już wszystko jasne, dziękuję Wam bardzo