Geometria analityczna Kawa: Punkt S(2,3) jest punktem przecięcia przekątnych równoległoboku ABCD orazAB→=[8,4],BC→=[2,6]. Oblicz: a) współrzędne wierzchołków równoległoboku, b)miarę kąta ABC c) promie okręgu opisanego na trójkącie ABC Próbuje policzyć pkt B. Uważam ze odległość od prostej AB punktu D to wysokość czy to prawda? Chce wyliczyć ze wzorów na pola miarę kata.

Kawa: Niech mi ktos pomoże xd

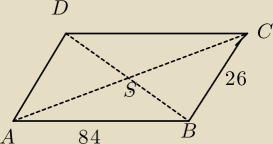
Aga1.: Rys pomocniczy bez układu współrzędnych A(x,_A,y_A) B(x_B,y_B) C(x_C,y_C) i D(x_D,y_D), AB→=[8,4] i AB→=[x_B−x_A, y_B−y_A] Stąd x_B−x_A=8 y_B−y_A=4 Podobnie rozpisz BC→, oraz AS→=SC→

Kawa: A jak policzyć miarę kata?

Kawa: Skąd masz te długości boków?

Aga1.: To nie są długości boków tylko AB→=[8,4] i BC→=[2,6] ( nie umiałam wpisać przecinka i nawiasu kwadratowego)

Aga1.: Albo inaczej AC→=2*AS→ i AC→=AB→+BC→ AC→=[8,4]+[2,6]=[10,10] 2*AS→=2*[2−x_A,3−y_A]=[4−2x_A,6−2y_A] [10,10]=[4−2x_A,6−2_yA] 4−2x_A=10 i 6−2y_A=10 dokończ.

Eta: → → AB=[8,4] , BC=[2,6] S(2,3) [x_B−x_A, y_B−y_A]=[8,4] ⇒ x_B−x_A=8 i y_B−y_A=4 [x_C−x_B, y_C−y_B]=[2,6] ⇒ x_C−x_B=2 i y_C−y_B=6 + −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− (* ) x_C−x_A=10 i y_C−y_A=10

	xA+xC
(**) oraz		=xS ⇒ xA+xC=4
	2

	yA+yC
		=yS ⇒ yA+yC=6
	2

to z (*) i (**) otrzymujemy : x_C=7 i y_C=8 ⇒ C(7,8) dokończ ...... i otrzymasz : A(−3,−2) , B(5,2), D(−1,4)

	AB o AD		2*8+6*4		√2
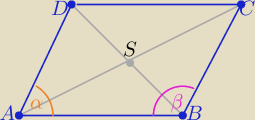
b) cosα=		=		= ........ =
	|AB|*|AC|		√80*√40		2

zatem α= 45^o to β=135^o c) z twierdzenia sinusów w ΔABC :

	|AC|
2R=		⇒........................ R=√34 [j]
	sinβ

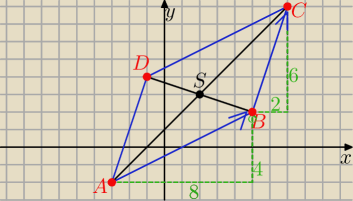
Eta: Dodam jeszcze Sprawdzenie w układzie współrzędnych ( wszystko ok)

Eta: → → Przy wyznaczaniu cosα ...... nad AB i DC ( wektory)