wykres trygonometria Metis: Mam problem z odczytaniem z wykresu rozwiazania Mam nierówność:

cos2x
	≥1 , gdzie x∊R−{kπ, k∊ℤ}
1−cos2x

cos2x
	≥1 /*sin2x
sin2x

cos²x≥sin²x cos²x−sin²x≥0 cos²x−(1−cos²x)≥0 cos²x−1+cos²x≥0 2cos²x≥1 /:2

	1
cos2x≥
	2

	1
Rysuję wykres f(x)=cosx i prostą y=
	2

	1
I odczytuje, kiedy wykres f(x) znajduje się nad prostą y=		.
	2

Wykres: http://wstaw.org/m/2015/09/12/Wykres.png

	π		π
Z wykresu: x∊[−		,		]
	4		4

	π		π
Rozwiązanie ogólne: x∊[−		+kπ,		+kπ] ,k∊ℤ
	4		4

	π		π
I uwzględniając warunek x∊R−{kπ, k∊ℤ} , mam: x∊[−		+kπ)∪[		+kπ) k∊ℤ
	4		4

Dobrze?

Nuti: Ten wykres jest błędny. Cała krzywa jest „skurczona" i przesunięta w górę po osi y. Cosinus ma wartości od −1 do 1, okres 2π miejsca zerowe co π..., a u ciebie ma tylko wartości nieujemne. Nie wiem, czy to wpływa na Twoje rozwiązanie −− tak mnie poruszył wygląd wykresu, że straciłam koncentrację −− ale to może wyjaśnić twój problem z odczytaniem z wykresu. Idź obejrzyj porządny wykres cosinusa na Wikipedii, może to coś zmieni.

Nuti: Zerknęłam na rozwiązanie:

	1
w momencie cos2x≥		powinienieś zastosować wzór skróconego mnożenia i rozpatrywać w
	2

dalszym ciągu

	√2		√2
(cosx −		)(cosx +		)≥0
	2		2

żeby na pewno czegoś nie ominąć. Albo oba czynniki mają być ujemne albo oba dodatnie.

Nuti: Twój wynik wydaje mi się poprawny, ale nie jest to ani zasługa wykresu, ani obliczenia. Nie wiem, jak do tego doszedłeś. Doszedłbyś do tego analizując iloczyn (jak w moim poprzednim poście) i poprawny wykres. Czekaj, chyba rozumiem − czy twój wykres miał być wykresem cosinus kwadrat?

Nuti: za bardzo jest zaokrąglony, wygląda jak przesunięty cosinus. Może trochę za dużo krzyku podniosłam cos²x powinien być trochę bardziej spiczasty w π/2 i co π.

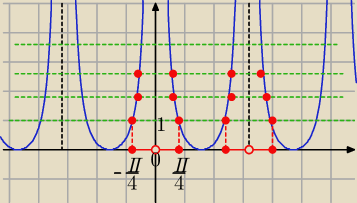Eta: f(x)= ctg²(x) i sin(x)≠0+kπ f(x)≥1 i sin(x)≠0

	π		π
x ∊< −		+kπ,		+kπ> \ {kπ} , k∊C
	4		4

Metis: Nuti tak, mój wykres to wykres funkcji f(x)=cos²x Eta jak otrzymałaś wykres funkcji ctg²x ? Moje przekształcenia są niepoprawne?

Nuti: @Eta skorzystała od razu w pierwszej linii z jedynki trygonometrycznej w mianowniku, stąd cotangens. Jeszcze raz sorry za zamieszanie w związku z wykresem − po głębszym zastanowieniu doszłam nawet do wniosku, że ten wykres nawet nie jest spiczasty, tylko trochę węższy niż cosinus... To wartość bezwzględna z cosinusa jest spiczasta

Nuti: @Metis Twoje przekształcenia są poprawne, tylko @Eta użyła innej metody. To kwestia gustu. Ja też bym wybrała sinus i cosinus, bo są bardziej... oswojone, ale można też operować tangensem i cotangensem, czemu nie. Otrzymaliście takie same wyniki, każde swoją metodą.

Metis: Nic się nie dzieje No tak...

cos2x
	≥1
sin2x

ctg²x≥1

Metis: Profesor przerobił całą trygonometrię na koniec roku szkolnego, gdy na lekcje chodziła jedna osoba. Teraz bez żadnej powtórki mam sprawdzian i sam muszę wszystko nadrabiać

Nuti: Pracujesz and tym przecież − dasz radę!

Eta:

5-latek: Czesc Michał Czy ja CI wyslalem materialy z rownann i nierownosci trygonometrycznych ?

Metis: Dobry Wieczór 5−latku Tak , wysyłales mi , i teraz często sobie do nich zaglądam , jak zdrowie 5−latku ? Dawno Cię nie widziałem na forum

5-latek: Wiesz miałem klopopty z komputerem i w tym tygodniu mielismy bardzo dużo pracy wiec byłem zmeczony

5-latek: Postaram CI się zrobić jeszcze z innej książki . Ale to na drugi tydzień .

Kacper: Metis mam nadzieję, że byłeś tą jedną osobą

Metis: Kacper niestety nie

Mila: Bardzo mądry Profesor.

Kacper: Przez takie zachowanie uczniów ciężko z materiałem się wyrobić

Metis: To nie tylko zachowanie uczniów . Gdyby wszyscy nauczyciele prowadzili lekcje tak jak w roku szkolnym to przychodzilibyśmy na zajęcia tak jak zawsze.

Braun: Na studiach to normalka, więc się przyzwyczajaj