 a)
Graniastosłup jest prawidłowy, więc w podstawie ma kwadrat. Bok tego kwadratu ma długość 4,
więc jego przekątna ma długość 4√2 (z twierdzenia Pitagorasa). Potrzebuję tej przekątnej, bo
występuje ona w trójkącie prostokątnym zbudowanym z przekątnej graniastosłupa i krawędzi
bocznej. Z tego trójkąta wyliczysz długość przekątnej graniastosłupa.
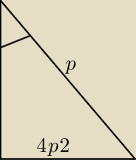
Oznaczam długość przekątnej graniastosłupa przez p i rysuję trójkąt, z którego można wyliczyć
to p. Na tym rysunku „4p2" oznacza 4√2 (nie udało mi się napisać tego lepiej!), a jedyny
oznaczony kąt to ten który ma 28 stopni.
Wyliczenie pochodzi z definicji sinusa kąta jako stosunku długości przeciwległej
przyprostokątnej do przeciwprostokątnej. Mamy:
a)
Graniastosłup jest prawidłowy, więc w podstawie ma kwadrat. Bok tego kwadratu ma długość 4,
więc jego przekątna ma długość 4√2 (z twierdzenia Pitagorasa). Potrzebuję tej przekątnej, bo
występuje ona w trójkącie prostokątnym zbudowanym z przekątnej graniastosłupa i krawędzi
bocznej. Z tego trójkąta wyliczysz długość przekątnej graniastosłupa.
Oznaczam długość przekątnej graniastosłupa przez p i rysuję trójkąt, z którego można wyliczyć
to p. Na tym rysunku „4p2" oznacza 4√2 (nie udało mi się napisać tego lepiej!), a jedyny
oznaczony kąt to ten który ma 28 stopni.
Wyliczenie pochodzi z definicji sinusa kąta jako stosunku długości przeciwległej
przyprostokątnej do przeciwprostokątnej. Mamy:
| 4√2 | |
=sin28 | |
| p |
| 4{2} | ||
p= | . | |
| sin28 |
| 4√2 | ||
p= | , źle mi się napisało. | |
| sin28 |
