Wyznaczyć przedziały monotoniczności i ekstrema funkcji cupid: Proszę o szybką pomoc Wyznaczyć przedziały monotoniczności i ekstrema funkcji

	x2 + 3x
f(x) =		dla x ≠ 1
	1 − x

Nuti: Dziedzina to R bez {1}. Policz pochodną, zbadaj znak (dodatnia − funkcja rośnie w przedziale, ujemna − funkcja maleje, zero i pochodna zmienia znak − ekstremum lokalne). Nie zapomnij zbadać granic lewo− i prawostronnej w 1. Poradzisz sobie dalej?

cupid: @Nuti a nie dasz rady rozwiązać :X ?

Nuti: Dałabym radę, ale miałam nadzieję, że już sobie poradzisz. Nie lubię tego edytora... Poczekaj trochę.

Nuti: Liczysz pochodną ilorazu (wzór: pochodna pierwszej razy wartość drugiej minus pochodna drugiej razy wartość pierwszej dzielone przez wartość drugiej do kwadratu):

	(2x+3)(1−x)−(−1)*(x2+3x)
f'(x)=		=
	(1−x)2

	−x2+2x+3
=
	(1−x)2

Rozkładasz licznik na czynniki (delta, pierwiastki − zwykłe równanie kwadratowe) i dostajesz

	−(x+1)(x−3)
f'(x)=
	(1−x)2

i badasz znak. Mianownik jest zawsze dodatni, więc to licznik określa znak pochodnej. Pochodna ma znak: nak pochodnejinus

Nuti: Coś mi się zacięło i musiałam wyjść z edycji. Cdn Na beznadziejnym rasunku jest znak pochodnej...

Janek191: @ Nuti : Kliknij poniżej na : rysuję

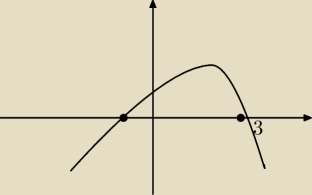
Nuti: No więc znak pochodnej: − dla x mniejszych od −1 0 dla x równego −1 + dla x między −1 a 3 (z wyjątkiem x równego 1, który jest spoza dziedziny) 0 dla x równego 3 − dla x większych od 3 Masz więc lokalne minimum w x=−1 (wartość −1) i lokalne maksimum w x=3 (wartość −9). Żeby policzyć ekstrema globalne, musisz policzyć: − granicę funkcji w minus nieskończoności − w plus nieskończoności − i granice lewo− i prawostronne w 1.

Nuti: granicę w plus i minus nieskończoności liczysz tak: przekształcasz wyrażenie wymierne dzieląc licznik i mianownik przez x:

x2+3x		x+3
	=
1−x		1   −1 x

Mianownik dąży w obu nieskończonościach do −1, a licznik do tej samej nieskończoności co x, czyli (po wymnożeniu z −1 z mianownika) dostajemy, że granica w minus niesk. jest plus niesk. a w plus niesk. to minus niesk. Czyli już wiesz, że ekstrema globalne nie istnieją. Policz jeszcze granice jednostronne w x równym 1, ale jestem pewna, że tam będzie asymptota pionowa.

Nuti: Granica w 1: licznik dąży do stałej (1+3=4), a mianownik dąży do zera − przez wartości ujemne z prawej strony 1, a przez dodatnie z lewej strony jedynki. Prosta x=1 st więc asymptotą pionową.

Kacper: Widzę, że ktoś gotowca wyciągnął

Nuti: Mam nadzieję, że nie popełniłam żadnego błędu walcząc z edytorem...

cupid: Dziękuję Ci Nuti

Nuti: A @Kacper się śmieje, że dałam się wrobić

Nuti: @Janek191 Da się tu zrobić cały wykres? Spróbowałam − wygląda na to, że się nie dało...