ciągi - monotonicznosc
Karolina: Ciąg an jest skonczony. Zbadaj monotonicznosc tego ciagu, jeśli:
{−n2 + 6 n − 5 dla n € N i n> 4
an=
{n+1 dla n € N i 4 ≤ n ≤ 10
10 wrz 22:04
Aga1.: Dobrze wszystko przepisałaś?
10 wrz 22:17
Karolina: Powinno być wzięte wszystko w klamrę razem do an . Ale nie umiałam tak zrobić. Wiesz o co mi
chodzi ?
10 wrz 22:19
Janek191:
Pewnie powinno być
− n2 + 6 n − 5 dla n ∊ℕ i n < 4
10 wrz 22:21
Janek191:
a1 = 0, a2 = 3, a3 = 4,
a4 = 5, a5 = 6, a6 = 7, a7 = 8, a8 = 9, a9 = 10, a10 = 11
10 wrz 22:24
Karolina: Przepraszam najmocniej . Faktycznie powinno być n < 4
10 wrz 22:27
Janek191:
To jaki jest ten ciąg ?

10 wrz 22:29
Karolina: Wiem, że powinno się odjąć an+1 − an żeby zbadać monotonicznosc. Ale jak w tym przypadku nie
mam pojęcia.
10 wrz 22:30
Janek191:
To nie widać,że ten ciąg jest rosnący ?

10 wrz 22:32
Karolina: Ciąg jest taki :
−n2 + 6 n − 5 dla n € N i n< 4
an=
n+1 dla n € N i 4 ≤ n ≤ 10
I te −n2+6 n... i n+1... w jedna klamrę do an

10 wrz 22:33
Karolina: Nie wiem po prostu jak z tym podwójnym rownaniem zrobić

10 wrz 22:34
Janek191:
Dla n < 4 liczysz an z górnego wzoru
a dla n ∊ { 4, 5,6,7,8,9,10 } liczysz an z dolnego wzoru.
Np, a1 = − 12 +6*1 − 5 = − 1 + 6 − 5 = 0
a5 = 5 + 1 = 6
10 wrz 22:37
Karolina: A co z tą zasadą: an+1 − an ?
10 wrz 22:43
Janek191:
Jest spełniona, bo
a2 − a1 = 3 − 0 = 3 > 0
a3 − a2 = 4 − 3 = 1 > 0
a4 − a3 = 5 − 4 = 1 > 0
itd. do końca
Ciąg (an) jest rosnący.
10 wrz 23:35
Karolina: Ok, dziękuję

A jeszcze zapytam, nie da się tego zrobić innym sposobem ?
10 wrz 23:50
Aga1.:
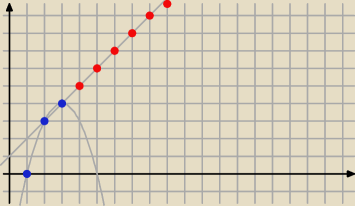
Inaczej? Możesz narysować wykres ( u mnie brakuje jednego punktu).
a
n+1−a
n liczysz, gdy masz ciąg nieskończony .
Chociaż czasami też warto obliczyć kilka początkowych wyrazów, by zauważyć, że ciąg nie jest
monotoniczny
11 wrz 07:30




 A jeszcze zapytam, nie da się tego zrobić innym sposobem ?
A jeszcze zapytam, nie da się tego zrobić innym sposobem ?
 Inaczej? Możesz narysować wykres ( u mnie brakuje jednego punktu).
an+1−an liczysz, gdy masz ciąg nieskończony .
Chociaż czasami też warto obliczyć kilka początkowych wyrazów, by zauważyć, że ciąg nie jest
monotoniczny
Inaczej? Możesz narysować wykres ( u mnie brakuje jednego punktu).
an+1−an liczysz, gdy masz ciąg nieskończony .
Chociaż czasami też warto obliczyć kilka początkowych wyrazów, by zauważyć, że ciąg nie jest
monotoniczny