aa Hugo: Udowodnij, że dowolną kwotę pieniędzy złożoną z n złotych (n ≥ 4) można wypłacic monetami 2 i 5 złotowymi. Ogólnie rozumiem problem ale chodzi o zapis formalny. Z indukcji matematycznej: T(k) dla 4zł = 2zl + 2zł Wartość = 2x + 5y, x,y ∊ N T(k+1) { dla 2k Wartość = 2x, k∊N //przyste { dla 2k+1 Wartość = 5 + 2x , k∊N //nieparzyste 4 = 2x = 2*2 = 4 5 = 5+2x = 5*2*0 = 5 6 = 2x = 2*3 = 6 7 = 5+2x = 5 + 2*1 = 7 Chodzi mi o zapis formalny, prosze o korekty Bo problem jest że nie wystarczy to rozumieć, trzeba to umieć także zapisać

PW: Formalnie trzeba pokazać, że równanie diofantyczne p·2 + q·5 = n ma rozwiązanie dla dowolnej liczby naturalnej n ≥ 4, i że rozwiązanie jest parą liczb naturalnych Oczywiście można na początek wspomnieć, że rozwiązanie dla parzystej n jest banalne i dalej zajmować się tylko nieparzystymi n.

:): inkducja! niedawno bylo juz takie zadanie tu 4=2*2+5*0 ok zakładamy, że n=2x+5y i pytamy czy istnieją x',y' : n+1=2x'+5y' 1=2*(−2)+5*1 1=2*3+5*(−1) n+1=2(x−2)+5(y+1) ///z założenia jak na początku x≥2 to koniec z drugiej strony x+1=2(x+3)+5(y−1) jeżeli więc y>1 to też ok zostaje tylko przypadek (x,y)=(0,1) oraz (1,1) ale wtedy n=5 ,n+1=2*3 ok lub n=7 wiec n+1=8=2*4

:): y≥1*** wiec wystarczy sprawdzić tylko (1,0) ..ale wtedy n=2 (a my rozpatrujemy n≥4) kONIEC

Hugo: @ Piękne rozwiązanie

Hugo: @PW A jak się rozwiązuje to rónanie dofantyczne? coś kojarze że się brało NWD(2,5) = 1

:): trzeba zgadanac 1 równanie.... a na wszystkei inne jest rozwiazanie..problem tylkow tym..ze rozwiazanai są CAŁKOWIte..nie naturalne..

:): rozwiązanei*

Hugo: Hugo nie rozumieć twojego posta ale zrozumieć tamto 17:06 Hugo myśleć że to mu wystarczać na Pt. rozsz euklidesa umiem : >

:): równanai diofantyczne są do rozwiazywanai równan typu a=bx+cy b,c,a dane tylko, że x,y mogą być UJEMNE Tez....

:): poczytaj gdzieś na necie o tym....to też ważny sposób

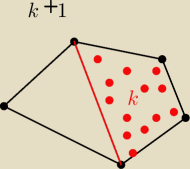
Hugo: poczytam ( : tu mam takie zadanie i podobnie go rozumiem kwestia zapisu Udowodni, ze suma kątów wewnętrznych w n−kacie wypukłym wynosi (n−2)π dla k = 1 ( trójkąt) (3−1)pi = 2pi , prawda (y) dla n = k (n−2)pi dla k + 1 Przyjmijmy sobie wielokąt k + 1 , łączymy w nim dwie krawędzie w taki sposób by tworzyły trójkąt. Trójkąt posiada (3−2)pi natomiast , druga figura utworzona z podzielonego k+1 − kąta towrzy nam k − kąt o wzorze (k−2)pi. Obydwie figury tworzą cały wielokąt. Zatem: (3−2)pi + (k−2)pi = pi + (k−2)pi = (k−2+1)pi = (k−1) pi czyli wielokąt dla k+1 wierzchołków Wykazałem? Jak to doprecyzować?

:): n=k (n−2)pi ...to bardzo zle wyglada

:): Powinieneś napsiać Z; suma kató wewnętrznych w n−kącie wypuklym wynoi (n−2)π

:): masz coś powiedzieć o n+1 ja bym go rozbił na 2.... o n−kątach i na trójkąt.. wiec taki ma (n−2)π (z zał) +π(trójkąt) czyli (n−2)π+π=(n−2+1)π=((n+1)−2)π KONIEC

Mila: Materiały (piękne) dla HUgo. http://knm.katowice.pl/licea/kolko/21.11.2011_beata_lojan/pliki/rownania_diofantyczne.pdf

:): spoko wyglądają Mila

Hugo: Mila Już się zabieram do lektury

Mila: math.uni.lodz.pl/~mzbanasz/Zadania_Inf/Teoria_liczb_przyklady.doc