Równania tryg Metis: Czy tenrozwiązany przykład jest dobrze rozwiązany? O.o 3ctg(2x+π)=−√3 /:3

	√3
ctg(2x+π)=−
	3

	π		√3
ctg(		)=
	3		3

	√3
ctg(2x+π)=−
	3

	π
2x+π=−		+kπ
	3

	4π
2x=−		+kπ
	3

	4π		kπ
x=−		+		, k∊Z
	6		2

	2π		kπ
x=−		+		, k∊Z
	3		2

Metis: Zła składnia na początku: Czy ten przykład jest dobrze rozwiązany? O.o

J: dobrze

Metis: Mam różne odpowiedzi

J: a jakie masz ?

Metis:

	π		kπ
x=−		+		, k∊Z
	6		2

Mila: Dobrze. Może w innym przedziale podana jest odpowiedź, napisz , co tam masz w książce.

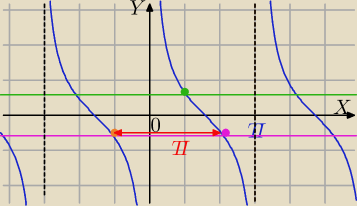
Mila: W niektórych podręcznikach podają rozwiązanie ujemne dla tgx i ctgx z przedziału (0,π) Pierwsza linijka:

	π
2x+π=(π−		)+kπ
	3

	π
2x=−		+kπ
	3

	π		kπ
x=−		+
	6		2

Metis: Dziękuje Milu

Mila:

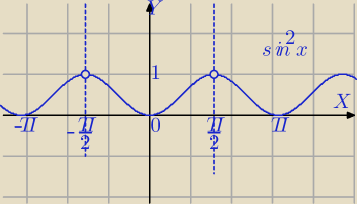
Metis: Mam taki postój z |sin²x|<1 , rozpisuję na podstawie definicji wartości bezwzględnej −1<sin²x<1 i nie wiem co zrobić teraz z tym wyrażeniem. Wykres?

Joe Black: Narysuj i pisz co widzisz

Mila: 0≤sin²x≤1 dla x∊R zrezygnuj z równości z prawej i będziesz w domu.

Metis: No tak, wszystko pięknie widać z wykresu Dziękuje Wam Muszę nabrać wprawy i pewności w tej trygonometrii bo czuję się w niej niepewnie.

Mila: To jaką dałeś odpowiedź?

Benny: Można tak? sin²x<1 1−sin²x>0 cos²x>0 itd.?

Godzio: Można

Metis: x=πk , k∊Z

Metis: Nie chyba źle

Joe Black:

	π
Wg mnie to x≠		+kπ, k∊Z
	2

Metis: http://wstaw.org/m/2015/09/08/1.png

Joe Black: nom

Mila: Mają być przedziały. To jest nierówność.

Joe Black: Czyli nie można pójść na łatwiznę

Metis: Nie wiem jak to zapisać

Joe Black:

	π		π
Np. x∊<kπ,		+kπ)u(		+kπ,π+kπ) , k∊Z ,tak Mila ?
	2		2

Metis:

	π
Czemu wyrzucasz		? Mam nierówność słabą.
	2

Joe Black:

	π
Bo |sin2x| ma być mniejsze od 1, a dla x=		−> |sin2x|=1
	2

Metis: Jasne Więc przedział który napisałeś jest chyba

Joe Black: Też mi się tak wydaję, ale jak się wypowie fachowiec to od razu inaczej

Mila: Dobrze Joe. Tylko na końcu nawias domknięty " >".

	π		π
Wyrzuca		, bo sin		=1
	2		2

Albo może tak:

	π		π
x∊(−		+kπ,		+kπ)
	2		2

Co masz Metisku w odpowiedzi?

Joe Black: Czemu na końcu domknięty ? Myślałem, że jak na początku dałem < to wystarczy... Bo jak wstawię > to znowu będzie początek... ale no widocznie tak trzeba

Metis: Milu to tylko część zadania. Z resztą nie miałem problemu. Tylko z wyznaczeniem dziedziny − kiedy dany ciąg jest zbieżny. Dziękuje jeszcze raz Tobie Milu , i Tobie Joe.

Mila: Dobranoc

Metis: Dobranoc