Rozwiąż jula : Przez środek boku trójkąta równobocznego poprowadzono prostą nachyloną do boku pod kątem α, gdzie α∊(0;90). W jakim stosunku ta prosta podzieliła pole trójkąta? Odpowiedź to: 2√3ctgα + 1

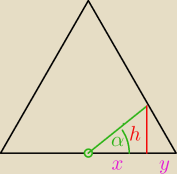
===: h/x=tgα ⇒ x= h/y=tg60^o ⇒ y= x+y=a/2 policzysz i porównasz pola

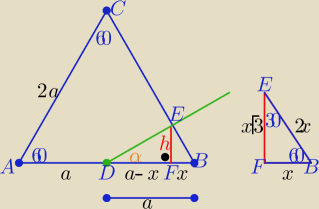Eta: P(ABC)=P=a²√3 , P(DBE)=P₁ ,

	P−P1		P
szukany stosunek pól to: k=		=		−1
	P1		P1

	1		ax√3
P1=		*2x*a*sin60o =
	2		2

	a2√3		2a
zatem k=		−1=		−1
	ax√3   2		x

	a−x		a
ctgα=		⇒a−x=x√3*ctgα ⇒a=x(√3ctgα+1) ⇒		=√3ctgα+1
	x√3		x

	2a
to k=		−1=2√3ctgα+2 −1=2√3ctgα +1
	x