W prostokątnym układzie współrzędnych wyznacz zbiór tych wszystkich punktów o ws ciasteczkoo: W prostokątnym układzie współrzędnych wyznacz zbiór tych wszystkich punktów o współrzędnych ( m, n) takich, że funkcja o wzorze f(x) = x²−2mx−n+1 ma dwa różne miejsca zerowe należące do przedziału (−1,1).

Nuti: Wydaje mi się, że to zadanie jest trudne, ale może się mylę. Umiem w każdy razie ograniczyć płaszczyznę wszystkich możliwych par (m,n) na płaszczyźnie do małego zbiorku, w którym jest zawarte twoje rozwiązanie, ale nie jestem pewna, czy zbiór rozwiązań nie jest jeszcze mniejszy. Wyjaśnię. Zbiór tych (m,n) na płaszczyźnie, których szukamy jest ograniczony następującymi warunkami: 1. Delta równania x²−2mx−n+1 musi być większa od zera (żeby równanie miało dwa różne pierwiastki). 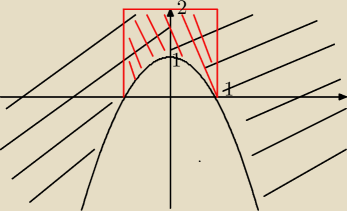Musi więc zachodzić 4m⁴−4(−n+1)>0 czyli m²+n−1>0 albo n>−m²+1 (zapisuję tak, żeby było widać, że to jest na płaszczyźnie (m,n) obszar nad parabolą n=−m²+1) nie wiem, czy umiem to narysować. Narysowałam. Warunek delta>0 spełniają punkty na obszarze zakreskowanym na czarno. 2. dwa pierwiastki muszą należeć do przedziału (−1,1). Spróbowałam to wyliczyć dokładnie, ale wyszła jakaś straszna funkcja uwikłana i stwierdziłam, że to chyba za trudne (do której klasy chodzisz?). Można użyć wzorów Viete'a, żeby przynajmniej ograniczyć zakreskowany obszar. Wzory Viete'a to w tym przypadku: x₁+x₂=2m x₁*x₂=−n+1. Skoro oba pierwiastki mają leżeć pomiędzy −1 a 1, to ich iloczyn też się musi mieścić w tym odcinku, a ich suma musi się mieścić między −2 a 2. To nam daje dwie nierówności na m i n: −2<2m<2 −1<−n+1<1 czyli −1<m<1 0<n<2 i dlatego zakreskowuję na czerwono część wspólną tego kwadratu (opisanego przed chwilką dwiema nierównościami na m i n) i obszaru nad parabolą. Rozwiązanie twojego zadania mieści się więc w całości w obszarze (BEZ brzegu!) zakreskowanym na czerwono, ale możliwe, że nie wszystkie punkty z tego obszaru spełniają warunki zadania.

J: https://matematykaszkolna.pl/forum/298504.html

J: @Nuti ... nie taka parabola

henrys: ona zrobiła parabolę nie dla tej funkcji tylko dla n=−n²+1

henrys: n=−m²+1

J: nie zwróciłem uwagi , ale i tak rozwiazanie jest mętne

henrys: trochę za dużo pisania i można się pogubić, ale wydaje mi się, ze jest ok. Nie rozumiem tylko dlaczego jakieś punkty z tego zakreskowanego obszaru miałyby nie spełniać warunków

J: a niby dlaczego suma ma należeć do przedziału (−2,2) ?

henrys: skoro −1<x₁<1 i −1<x₂<1 to x₁+x₂ ∊(−2,2)

henrys: trzeba chyba jeszcze dodać ten warunek f(1)>0 i f(−1)>0

J: popatrz do linku 12:52 ... te warunki wystarczają

henrys: tak, tylko to rozwiązanie też jest dobre, tyle, że trochę jak napisałeś "mętne" no i niepełne.

Nuti: @henrys Niektóre punkty z obszaru mogą nie spełniać warunków, bo przy stosowaniu wzorów Viete'a posługuję się implikacją w jedną stronę: [x₁, x₂ należą do (−1,1)] => [x₁*x₂ należy do (−1,1) i x₁+x₂ należy do (−2,2)] ale implikacja odwrotna (której tak naprawdę potrzebujemy w zadaniu żeby się upewnić, gdzie są

	8		10
nasze pierwiastki) nie jest prawdziwa, weź na przykład x1=		i x2=		. Iloczyn
	10		9

tam gdzie trzeba, suma tam gdzie trzeba, ale jedna z liczb jest spoza (−1,1).

Nuti: @J co to jest x_w w linku 12:52? Ktokolwiek, kto wie: Dla której klasy jest to zadanie?

J: x_w , to współrzędna wierzchołka paraboli i musi leżeć pomiędzy: x₁ i x₂

Nuti: Widzę, że znowu się rozgadałam... To, co napisałam o 07:54, powinno zostać sformułowane w następujący sposób: użyłam warunku koniecznego zamiast dostatecznego (wystarczającego) dla pierwiastków na znajdowanie się między −1 a 1. x_w to x−owa wierzchołka paraboli, tak? Sprawdzę, w jaki sposób warunki z linku ograniczają „mój" obszar. Wasze rozwiązanie jest istotnie dużo lepsze, nie wpadłam na nie.

Nuti: @J dzięki, najpierw napisałam komentarz, a dopiero później odświeżyłam stronę...

Nuti: O, bardzo mocno go ogranicza

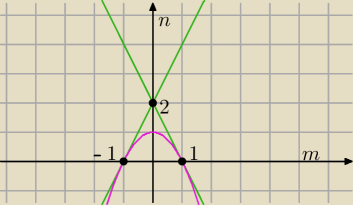
J: Szykany obszar, to obszar zawarty nad parabolą i pod prostymi

henrys: swoją drogą, to zadanie dla licealisty może być bardziej problematyczne niż się wydaje (właśnie poprzez określenie warunków koniecznych i dostatecznych)

Nuti: @J zgadza się, ale trzeba dodać, że tylko część dla n>0 (lub, równoważnie, dla m między −1 a 1), bo pod osią m też są dwa obszary, które można opisać jako „nad parabolą i pod prostymi".

J: racja ... mało precyzyjnie opisałem obszar

Nuti: @henrys Racja!