Trafiłem przypadkiem na takie zadanie i zupełnie nie mogę znaleść rozwiązania :/ Voldius: Prosta k jest styczna do okręgu o środku O, punkcie A. Wyznacz miarę kąta zawartego między styczną i cięciwą AB okręgu, gdzie B jest punktem na okręgu, wiedząc, że kąt ACB=44⁰ i C jest punktem na okręgu.

Janek191: Popraw treść zadania

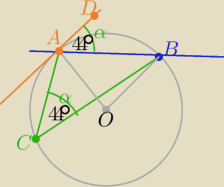
Eta: Szukany kąt , to kąt "dopisany" jego miara = mierze kąta wpisanego opartego na łuku AB zatem |∡BAD|=|∡ACB|=44^o

Voldius: Właśnie o takim podejściu myśałem, ale żeby było to możliwe czy styczna nie musi być równoległa do odcinka |CB|?

Janek191: Musi, ale Ecie trochę nie "wyszedł " rysunek

Voldius: Hah OK, dzięki za pomoc 😃

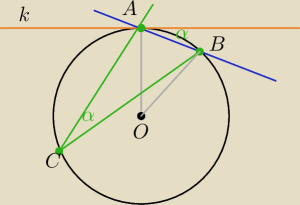
Aga1.: styczna nie musi być równoległa do CB.

Janek191: I ∡ AOB I = 2 α ⇒ I ∡ OAB I = 90^o − α ⇒ miara szukanego kąta = α