twierdzenie Bayesa, prawdopodobieństwo warunkowe Bayess: Witam, proszę o pomoc w rozwiązaniu zadania. Z dwóch urn zawierających kolejno: 2 kule białe i 3 czarne oraz 3 kule białe i 2 czarne losujemy niezależnie po jednej kuli. Następnie wylosowane kule wkładamy do trzeciej urny − dotychczas pustej. Losujemy jedną kulę z trzeciej urny − okazała się biała. Jakie jest prawdopodobieństwo wylosowania z trzeciej urny dwóch białych kul? Nie wiem czy dobrze zrozumiałam to zadanie. Czy mogę to rozwiązać za pomocą drzewka stochastycznego, a później prawdopodobieństwa warunkowego Każda odpowiedź mile widziana

Kacper: Wystarczy drzewko stochastyczne. Masz odpowiedź do zadania?

Bayess: Nie mam poprawnej odpowiedzi. Czyli drzewko, że w I losowaniu prawdopodobieństwo wylosowania 2 białych jest 6/25, dwóch czarnych 6/25, a białej i czarnej 13/25. Co dalej

Bayess: Prawdopodobieństwo, że w III urnie były dwie białe kule to 6/19

Kacper: Prawdę mówiąc, to w treści zadania brakuje informacji ile razy losujemy z trzeciej urny. Jeśli dwa razy, to przecież informacja, że za pierwszym razem wylosowano białą i tak nie zmieni wyniku, bo takie zdarzenie musiało zajść.

Bayess: Przepraszam, pomyliłam ostatniie zdanie. Chodziło o prawdopodobieństwo, że w trzeciej urnie są 2 kule białe.

Kacper: To w takim razie prawdopodobieństwo warunkowe.

Bayess: Prawdopodobieństwo wylosowania 2 białych kul/prawdopodobieństwo wylosowania co namniej jednej białej kuli 6/25/19/25

Kacper: Ja muszę uciekać, będę wieczorem. W tym czasie może ktoś pomoże.

Bayess: Ma ktoś jakiś pomysł na to zadanie

Bayess: Odnawiam

Mila: Może przepisz dokładnie treść z książki.

Bayess: Z dwóch urn zawierających kolejno: pierwsza urna − 2 białe i 3 czarne kule, a druga urna 3 białe i 2 czarne kule losujemy niezależnie po jednej kuli. Wylosowane kule wkładamy do trzeciej urny, która dotychczas była pusta. Następnie wylosowaliśmy jedną kulę z trzeciej urny. Okazała się biała. Jakie jest prawdopodobieństwo, że w trzeciej urnie były dwie białe kule?

Mila:

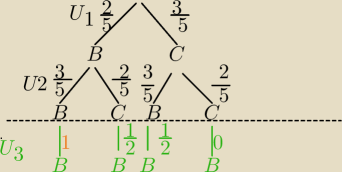
	2		3		2		2		1		3		3		1
P(B)=		*		*1+		*		*		+		*		*		+0
	5		5		5		5		2		5		5		2

	6		4		9		25		1
P(B)=		+		+		=		=
	25		50		50		50		2

	2   3   * *1 5   5		6		12
P(BB/B)=		=		*2=
	1   2		25		25

Taka masz odpowiedź?

Bayess: Dziekuje za pomoc. Rozumiem Twoje rozwiązanie. Nie mam odpowiedzi w książce, mi wyszło 6/19. Zrobiłam tak jak Ty drzewko stochastyczne do losowania z dwóch urn, a później policzyłam prawdopodobieństwo warunkowe. zrobiłam tak (6/25)/(19/25)=6/19, 6/25. prawd. że są dwie białe, a 19/25 prawd. że nie ma żadnej czarnej. Kiedy moje rozwiązanie byłoby poprawne

Bayess: Co policzyłam? czego nie wzięłam pod uwagę w obliczeniach/?

Mila: Skąd ta 19?

Bayess: 19/25 to suma prawdopodobieństw wylosowania z urn dwóch białych (6/25) lub białej i czarnej (13/25)

Mila: Napisz działanie z którego to policzyłeś.

Bayess: 6/25+9/25+4/25

Mila: To nie jest całe zdarzenie, musisz dołączyć trzecie losowanie. Masz przebieg doświadczenia na drzewku.

Bayess: Ok, dziękuję za pomoc

Mila: