parametr, rownanie trygonometryczne
albus54: wyznacz wartości parametru m dla których równanie ∫ tgx − 1 ∫ = m
2 − 6m ma dwa rozwiążania w
przedziale <0, pi> ( to ∫∫ to wartość bezwzględna tylko nie wiem jak to wpisać ).
Po pierwsze określiłem dla jakich m równanie głowne ma w ogole rozwiazania i wyszło mi, ze dla
m ∊ ( −
∞ , 0> ∪ < 6, +
∞). Teraz pewnie trzeba posłużyć się wykresem tangensa, przesunietym o 1
w prawo i odbitym symetrycznie od osi OX ( wartsc bezwzględna ) ale nie wiem jak wyznaczyć
dokładne wartości. Ktoś pomoze? dzieki

5 wrz 20:43
5-latek : |tgx−1|= m2−6m
5 wrz 20:51
Mila:
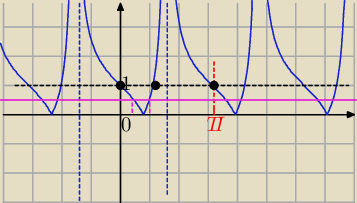
0<m
2−6m<1 dwa rozwiązania w przedziale <0,π>
5 wrz 21:13
albus54: ?
5 wrz 21:17
albus54: co teraz?
5 wrz 21:17
Mila:
O co chodzi?
5 wrz 21:17
Mila:
Masz rozwiązać podaną nierówność.
Przesuwając różową linię w górę od zera do 1 to przetnie wykres w dwóch punktach.
⇔są dwa rozwiązania dla x∊<0,π>
5 wrz 21:20
albus54: no bo taki wykres tez sobie narysowałem, wiem za ma byc nierownosc jak napisales, ale
rozwiazanie z tylu zbioru to: m∊ ( 3 − √10, 0 ) ∪ ( 6, 3 + P{10} )
5 wrz 21:20
albus54: a tak w ogóle to dlaczego ta nierownosc jest od 0 do 1 a nie wieksze lub rowne od 0, jak to
przy warotsc bwzgl. z tangensa?
5 wrz 21:22
albus54: rzeczywiscie, wychodzi, jak taka nierownosc sie rozwiazuje. ale skad ona sie wziela,
wytlumaczysz? dzieki
5 wrz 21:24
Mila:
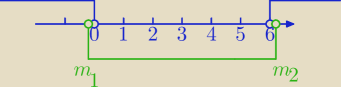
m
2−6m>0 i m
2−6m<1
m(m−6)>0 i m
2−6m−1<0⇔Δ=36+4=40,
√40=2
√10(parabole skierowane do góry)
| | 6−2√10 | | 6+2√10 | |
m=0 lub m=6 , m1= |
| =3−√10 , m2= |
| =3+√10⇔ |
| | 2 | | 2 | |
(m=0 lub m=6 , m
1≈−0.16, m
2≈6.16)
m∊(3−
√10,0)∪(6,3+
√10)
5 wrz 21:33
Mila:
Nie rozwiązywałeś graficznie równań z parametrem?
y=m2−6m to jest stała wartość (graficznie masz jeden przykład − różowa linia), o 21:21
napisałam
5 wrz 21:36
albus54: Mila, wytłumaczysz mi jeszcze dlaczego roziwazujemy rownianie 0<m2−6m<1 a nie m2 − 6m ≥ 0?
5 wrz 21:40
Mila:
Patrz na wykres i przesuwaj linijkę od dołu do góry.
( bierzesz pod uwagę wykres tylko dla podanego przedziału.)
Gdy y=0 to wykres będzie przecięty w jednym punkcie.
Gdy y=1 to wykres będzie przecięty w trzech punktach ( czarne).
5 wrz 21:42
Mila:
Narysować jeszcze raz z zaznaczeniem punktów przecięcia, czy już sam zauważyłeś.?
5 wrz 21:44
albus54: widze to, ale gdy y > 1 to co? tez 2 razy
5 wrz 21:51
Mila:
y>1 to masz trzy punkty przecięcia.
5 wrz 21:55
albus54: w przedziale od 0 do pi widze tylko 2
5 wrz 21:57
Aga1.: Witaj Mila.
Dla y>1 oj chyba 2
5 wrz 21:57
Mila:
Dziękuję Aga, witam ciepło.
Oj, dwa − przejechałam przedział na zachód na ujemne. Dobrze Albus widzisz.
5 wrz 22:02
albus54: To jak w koncu ma byc? Bo jak jest rownanie |tgx−1|= m2−6m to wedlug mnie trzeba to robic tak:
m2−6m ≥ 0. i pozniej s[rawdzic gdzie prosta rownolegla do osi OY przecina wykres funkcji
|tgx−1| 2 razy. ale cos nie działa
5 wrz 22:13
albus54: aa no i sprawdzic czy to nalzezy do przedziału ktory wyszedł z m2−6m ≥ 0.
5 wrz 22:13
Mila:
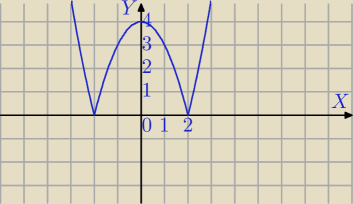
Rozwiąż .
Ile rozwiązań ma równanie
|x
2−4|=m w zależności od wartości parametru
m?
Narysuję Ci wykres .
5 wrz 22:13
albus54: jak m < 0 to 0 . jak rowne 0 to 2 . jak od 0 do 4 otwarty przedział to 4. jak 4 to 3 jak wiecej
niz 4 to 2 rozwiazania
5 wrz 22:15
Mila:
Zaraz napiszę jeszcze raz.
5 wrz 22:21
Mila:
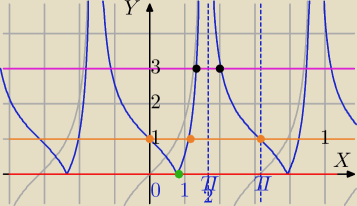
1) m
2−6m>0 i m
2−6m<1
⇔
m∊(3−
√10)∪(6,3+
√10)
lub
2)
m
2−6m>1
m
2−6m−1>0⇔
m<3−
√10 lub m>3+
√10
Cd za chwilę.
5 wrz 22:31
Mila:
22:15 dobrze.
5 wrz 22:32
Mila:
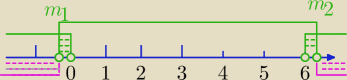
Dwa rozwiązania :
m∊(−
∞,3−
√10)∪(3−
√10,0)∪(6,3+
√10)∪(3+
√10,
∞)
Jeśli m
2−6m=0 masz jedno rozwiązanie .
|tg(x)−1|=0
tgx=1
Jeśli m
2−6m=1 masz 3 rozwiązania:
|tgx−1|=1
tgx−1=1 lub tgx−1=−1
tgx=2 lub tgx=0
x=arctg(2) lub x=0 lub x=π
Trzeci przypadek rozwiąż sam:
5 wrz 22:49
albus54: jaki to ma byc w ogole przypadek? mozes tak ogolnie opisac slownie co sie tu po kolei robi? nie
musisz liczyc bo sobie policze, tylko tak ogolnie napisac o co chodzi i po co sie co robi.
6 wrz 19:41

 0<m2−6m<1 dwa rozwiązania w przedziale <0,π>
0<m2−6m<1 dwa rozwiązania w przedziale <0,π>
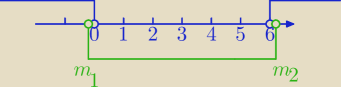 m2−6m>0 i m2−6m<1
m(m−6)>0 i m2−6m−1<0⇔Δ=36+4=40, √40=2√10(parabole skierowane do góry)
m2−6m>0 i m2−6m<1
m(m−6)>0 i m2−6m−1<0⇔Δ=36+4=40, √40=2√10(parabole skierowane do góry)
 Rozwiąż .
Ile rozwiązań ma równanie
|x2−4|=m w zależności od wartości parametru m?
Narysuję Ci wykres .
Rozwiąż .
Ile rozwiązań ma równanie
|x2−4|=m w zależności od wartości parametru m?
Narysuję Ci wykres .
 1) m2−6m>0 i m2−6m<1
⇔
m∊(3−√10)∪(6,3+√10)
lub
2)
m2−6m>1
m2−6m−1>0⇔
m<3−√10 lub m>3+√10
Cd za chwilę.
1) m2−6m>0 i m2−6m<1
⇔
m∊(3−√10)∪(6,3+√10)
lub
2)
m2−6m>1
m2−6m−1>0⇔
m<3−√10 lub m>3+√10
Cd za chwilę.
 Dwa rozwiązania :
m∊(−∞,3−√10)∪(3−√10,0)∪(6,3+√10)∪(3+√10,∞)
Jeśli m2−6m=0 masz jedno rozwiązanie .
|tg(x)−1|=0
tgx=1
Dwa rozwiązania :
m∊(−∞,3−√10)∪(3−√10,0)∪(6,3+√10)∪(3+√10,∞)
Jeśli m2−6m=0 masz jedno rozwiązanie .
|tg(x)−1|=0
tgx=1