Planimetria Medyk : Długość jednego z boków trojkata jest równa 6 a cosinus kata leżącego przy tym boku wynosi 1/3. Oblicz promień okręgu wpisanego w ten trojkat, jeżeli promień okręgu na nim opisanego jest równy 9.

Eta:

	1		2√2
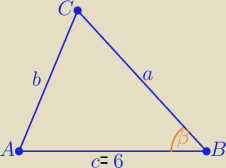
c=6 , R= 9 , cosβ=		⇒ sinβ= √1−19=
	3		3

z tw. sinusów

b
	=2R ⇒ b=2R*sinβ=......
sinβ

z tw. kosinusów : b²=c²+a²−2ac*cosβ ⇒ ........ a=20

	a+b+c		2P
P=rp , p=		⇒ r=
	2		a+b+c

	1
P=		ac*sinβ
	2

to r=.................. dokończ