Geometria Dominika: Hej, problem z geometrią analityczną Styczne do okręgu x²+y²=5 w punktach S i T przecinają się w punkcie (−5,−5). Oblicz odległość między punktami S i T Odpowiedź: 3√2

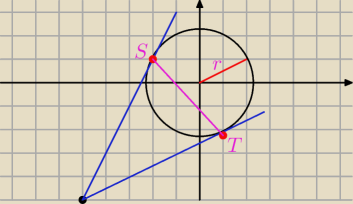Aga1.: Interpretacja geometryczna

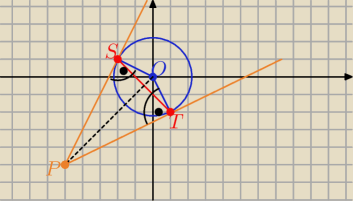Eta: |OP|=5√2 , |OT|=OS|=r=√5 Z tw. Pitagorasa |OP|=√50−5= 3√5

	|OP|*|ST|
Pole deltoidu (PTOS)=		= 2*P(ΔPTO)
	2

to

	4p(ΔPTO)		2*3√5*√5		6
|ST|=		=		=		= 3√2
	|OP|		5√2		√2

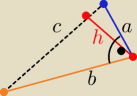Eta: 2 sposób

	a*b
h=
	c

	√5*3√5		3√2
|ST|= 2h , h=		=
	5√2		2

|ST|=2h=3√2

Aga1.: PT=3√5