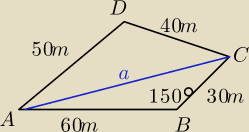
Działka budowlana ma kształt nieregularnego czworokąta Tyryryr: Działka budowlana ma kształt nieregularnego czworokąta. Wyniki pomiarów wykonanych przez geodetę są przedstawione na rysunku. Oblicz pole powierzchni tej działki. Podaj wynik przybliżony z dokładnością do 1 m² Wiem, że muszę podzielić ten czworokąt na dwa trójkąty. Tak też zrobiłam. I obliczyłam pole trójkąta ABC: P = ¹₂ * 60 * 30 * sin 150 st. Wyszło 450 m² I teraz zaczyna się mój problem, gdyż nie wiem co mam zrobić. Próbowałam wyliczyć a z twierdzenia cosinusów, ale wychodzi mi bardzo dziwny wynik. mianowice, że a= 30 √5 + 30 √2 √3 Czy ktoś mógłby mi pomóc?

Aga1.: Wyszło Ci a²=4500+1800√3?

Janek191: P₁ = 0,5*60*30*sin 150^o = 900*0,5 = 450

	√3
a2 = 602 + 302 − 2*60*30*cos 150o = 3600 + 900 − 3 600* (−		) = 4500 + 1800 √3 =
	2

≈ 4 500 + 3 114 ≈7 614 oraz a² = 50² + 40² − 2*50*40*cos δ = 2500 + 1600 − 4000*cos δ 7 614 = 4 100 − 4000*cos δ 4000 cos δ = − 3 514 cos δ = − 0,8785 cos²δ = 0,7718 sin²δ = 1 − 0,7718 = 0,2282 sin δ = 0,4777 P₂ = 0,5*50*40*0,4777 =477,7 ≈ 478

PW: Poprzestałbym na policzeniu a². Następnie − korzystając z faktu, że trójkąty ABC i ABD mają jednakowe obwody − obliczyć stosunek ich pól posługując się wzorem Herona. Obwody są jednakowe, więc ten stosunek nie będzie taki koszmarny − coś się skróci.

hh: w odpowiedziach jest ≈920m

Mila: Tak jak u Janka, tylko bez obliczania √3 przy wartości a². 4500+1800√3=2500+1600−2*50*40* cos ∡D 400+1800√3=−4000*cos ∡D 4+18√3=−40*cos ∡D 2+9√3=−20*cos ∡D

	2+9√3
cos ∡D=−		≈0.879≈0.88
	20

sin²∡D≈1−0.88² sin∡D≈0.47

	1
PΔACD≈		*40*50*0.47=470
	2

P_ABCD≈470+450=920 =================

janek191: