równania wymierne marcik: Proszę o pomoc z tym przykładem |^−x_x+1|=−|x| rozwiązaniem ma być x=0

marcik: Bardzo proszę o pomoc!

Eta: założenie x≠ −1 i |−x|=|x| |x|= −|x|*|x+1| ⇒ |x|(1+|x+1|)=0 ⇒ |x|=0 lub |x+1|=−1 −− sprzeczność zatem |x|=0 ⇒ x=0

Mila: Dla x≠−1 mianownik różny od zera. Lewa strona równania :

	−x
|		|≥0
	x+1

Prawa strona równania: −|x|≤0 stąd wniosek: Obie strony równania równe zero i x≠−1⇔x=0 (licznik równy 0 wtedy i prawa strona równania jest równa 0))

Janek191:

	−x
I		I = − I x I
	x + 1

I −x I
	= − I x I , dla x ≠ 0 dzielimy przez − I x I
I x + 1 I

1
	= 1 ⇒ x = 0 − sprzeczność lub x = − 2 też sprzeczność
I x + 1I

Dla x = 0 mamy

	0
I		I = − I 0 I
	0 + 1

0 = 0 Odp. x = 0 =======

Eta:

marcik: Dziękuję

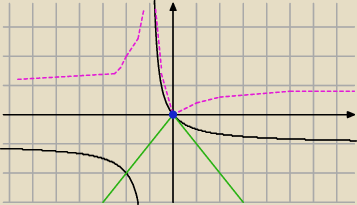
Aga1.: Można też rozwiązać graficznie.W tym przypadku nie jest to metoda najszybsza.