Geometria analityczna
Agata: Dany jest zbiór F={(x,y): |x|+|y|=4}. Okrąg o środku O(0,0) i promieniu r ma ze zbiorem F osiem
punktów wspólnych. r=?
Poprawna odpowiedź to przedział (2√2;4)
3 wrz 22:42
Mila:
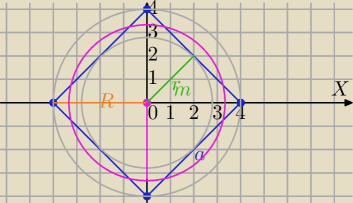
a=4
√2
| | 1 | |
rm= |
| a=2√2 promien okręgu wpisanego w kwadrat |
| | 2 | |
R=4 promień okręgu opisanego na kwadracie.
2
√2<r<4
3 wrz 22:54
Janek191:
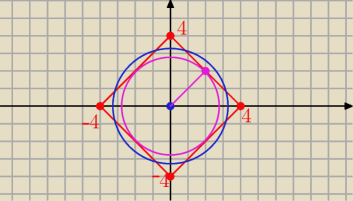
3 wrz 22:56
Janek191:
Za długo się grzebałem

3 wrz 22:57
Agata: Dlaczego zbiorem punktów jest kwadrat, czy wyjaśniłby mi to ktoś ?

4 wrz 20:56
looomp:
zbiór F to kwadratowa ramka
4 wrz 20:59
Mila:
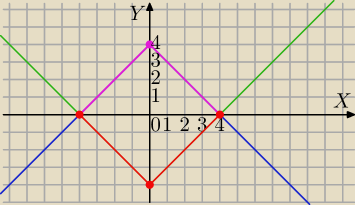
|x|+|y|=4
1)
|y|=y dla y≥0 (punkty wykresu na osią OX) wtedy masz równanie:
|x|+y=4
y=−|x|+4
2) |y|=−y dla y<0 (punkty wykresu pod osią OX) wtedy masz równanie:
|x|−y=4
y=|x|−4
4 wrz 21:03
Agata: Dziękuję za pomoc

4 wrz 21:07
Mila:
4 wrz 21:07
 a=4√2
a=4√2



 |x|+|y|=4
1)
|y|=y dla y≥0 (punkty wykresu na osią OX) wtedy masz równanie:
|x|+y=4
y=−|x|+4
2) |y|=−y dla y<0 (punkty wykresu pod osią OX) wtedy masz równanie:
|x|−y=4
y=|x|−4
|x|+|y|=4
1)
|y|=y dla y≥0 (punkty wykresu na osią OX) wtedy masz równanie:
|x|+y=4
y=−|x|+4
2) |y|=−y dla y<0 (punkty wykresu pod osią OX) wtedy masz równanie:
|x|−y=4
y=|x|−4
