Oblicz Natalia: |x+3| + |x−2| gdy x nalezy do (−∞;−3) Zapisz wyrażenie w najprostszej postaci bez użycia symbolu wartości bezwzględnej.

Janek191: x ∊ (−∞ ; − 3) ⇒ x + 3 < 0 ⇒ I x + 3 I = − (x + 3 ) = − x − 3 oraz x − 2 < 0 ⇒ I x − 2 I = −( x −2) = − x + 2 więc I x + 3 I + I x − 2 I = ( − x − 3) + ( − x + 2) = − 2 x − 1

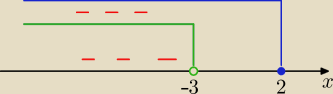
Eta: Dla x∊(−∞, −3) obydwa wyrażenia pod modułami zmieniają znaki |x+3|+ |x−2| = −x−3−x+2 = −2x−1

Janek191: A Natalia już śpi ?

Natalia: Tak poszłam już spać wczoraj Dzięki za pomoc !

teusz: Dobry wieczór Mam pytanie odnośnie postu Janka z 22:21 x+3<0 jest dlatego mniejsze od 0 ponieważ przedział zawiera liczby mniejsze od 3 gdyż przedział nie jest zakończony ">" (zamknięty?) wiec nie może być mniejsze bądź równe 0, tak? Mam nadzieje ze dobrze wytłumaczyłem o co chodzi w moim zapytaniu

Aga1.: Ix+3I=x+3, gdy x+3≥0 Ix+3I=−(x+3), gdy x+3<0, czyli x<−3 , czyli x∊(−∞,−3)