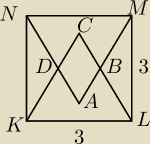
Uzasadnij, że |AC|=3(p{3}-1) i |DB|=3-p{3}. nacix: W kwadrat KLMN, którego bok ma długość 3, wpisano dwa trójkąty równoboczne w sposób pokazany na rysuku. Uzasadnij, że |AC|=3(√3−1) i |DB|=3−√3.

PW: Wskazówka: dwie wysokości opisanych trójkątów dawałyby wysokość kwadratu, gdyby nie to, że sumując wysokości trójkątów dwa razy liczymy długość odcinka AC.

nacix: a co z odcinkiem |DB|?

magik:

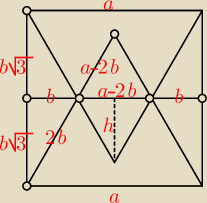
	√3
a = 3, 2b√3 = 3, b =
	2

PW: Jest równoległy do podstawy trójkąta i wisi "w połowie kwadratu" (mam nadzieję, że umiesz to uzasadnić powołując się na pewne symetrie). Skoro wiemy jak dzieli wysokość przed chwilą policzoną, to i wiemy jaki jest stosunek jego długości do długości podstawy (mówiąc prosto: podstawa małego trójkąta do podstawy dużego ma się tak, jak wysokość małego do wysokości dużego).

Eta:

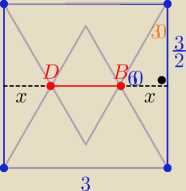
	1
x=		√3 to |DB|=3−2x=............
	2

wykazanko: Wykaż, że ten czworokąt jest rombem.

Eta: Długości boków są równe i przekątne są prostopadłe i mają różne długości więc czworokąt jest rombem