Extrema
Nju: Jak sprawdzić czy i ile funkcja ma minimów/maximów lokalnych?
3 wrz 20:23
J:
a jaka funkcja ?
3 wrz 20:24
Nju: obojętnie, nie chce rozwiązania, chcę metodę. Może być dla przykładu f(x)=x5+5x−1
3 wrz 20:46
PW: Jakie pytanie, taka odpowiedź:
1. Wytypować podejrzanych.
2. Zweryfikować podejrzenia.
Taka policyjna metoda sprawdza się w praktyce.
3 wrz 20:47
J:
pytałem, o ilość zmiennych...
Dla funkcji jednej zmiennej liczysz pierwszą pochodną...tam,gdzie się zeruje, może być
ekstremum (ale nie musi ), aby było, pochodna w tym punkcie musi zmieniać znak
3 wrz 20:49
Janek191:
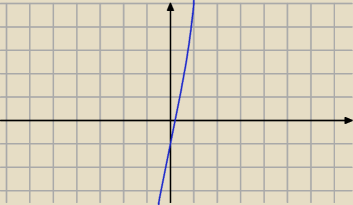
f '(x) = 5 x
4 + 5 ⇔ 0 ⇔ 5 x
4 = − 5 ⇔ x
4 = − 1 − sprzeczność
Ta funkcja nie ma ekstremów

3 wrz 20:49
ICSP: Sama pochodna to niestety za mało.
3 wrz 20:50
Nju: No na maturze próbnej takie jedno dostałem i szukam jak w łatwy sposób mogę sobie to jakoś w
głowie ułożyć by potem już szybciej trochę robić takie zadania. Jak to robić.
3 wrz 20:53
J:
Witaj ICSP .... bez przesady, chodzi o schemat
3 wrz 20:54
J:
1) liczysz pochodną
2) przyrównujesz do zera
3) badasz zmiane znaku w punkcie zerowania lub,
4) liczysz drugą pochodną w tym punkcie i:
jeśli jest dodatnia , to masz minimum, jesli ujemna , maksimum
3 wrz 20:57
Nju: a skąd wiedzieć czy funkcja ma więcej minimów/maximów niż jedno?
3 wrz 21:01
J:
bo pochodna może się zerować w więcej niż jednym punkcie
3 wrz 21:02
Nju: dalej nie rozumiem, mógłbyś jakiś przykład podać?
3 wrz 21:08
J:
Jesli będziesz miał wielomian trzeciego stopnia, to pochodna będzie trójmianem kwadratowym,
który może zerować się w dwóch punktach i tam mogą być ekstrema
3 wrz 21:10
PW: f(x) = x3+4x2+4x
3 wrz 21:11
J:
..bardzo dobry przykład dał PW ... policz ekstrema
3 wrz 21:13
Janek191:
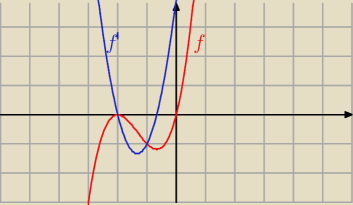
3 wrz 21:15
J:
popatrz na wykresy Janka .. .tam gdzie pochodna się zeruje ( niebieska), tam funkcja
(czerwona) ma ekstrema... a Ty je oblicz
3 wrz 21:17
 f '(x) = 5 x4 + 5 ⇔ 0 ⇔ 5 x4 = − 5 ⇔ x4 = − 1 − sprzeczność
Ta funkcja nie ma ekstremów
f '(x) = 5 x4 + 5 ⇔ 0 ⇔ 5 x4 = − 5 ⇔ x4 = − 1 − sprzeczność
Ta funkcja nie ma ekstremów 
