Wynik zaokraglij do pierwszego miejsca po przecinku piotrek prosi o pomoc : Oblicz pole rownolegloboku o przekatnych 10 i 6 oraz kacie miedzy nimi rownym 40 stopni. Wynik zaokraglij do pierwszego miejsca po przecinku

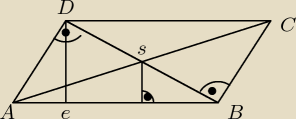
R.W.16l: dla sprostowania, umieszczę pełny opis AB || DC |AB|=|DC| DA || CB |DA|=|CB| jako, że przekątne dzielą się na pół, to: |AC|=10 |AS|+|SC|=10 |AS|=|SC| 2|AS|=2|SC|=10 |AS|=|SC|=5 |DB|=6 |DS|+|SB|=6 |DS|=|SB| 2|DS|=2|SB|=6 |DS|=|SB|=3 Kąt DSA = Kątowi BSC = 40 stopni, czyli:

	360 stopni − Kąt ASD − Kąt CSB		360 stopni − 80 stopni
Kąt DSC = Kątowi ASB =		=		=
	2		2

	280
		stopni = 140 stopni
	2

	ah
Wzór na pole trójkąta =
	2

Pole trójkąta ASB = Polu trójkąta DSC Pole trójkąta ASD = Polu trójkąta BSC Pole trójkąta ADB = Polu trójkąta DCB Trójkąt BSC (ale także trójkąt DSA) a=3 (|SB|) h=√|SC|²−|SB|²=√25−9=4

	3*4
Pole trójkąta BSC = Pole trójkąta DSA =		= 6
	2

|CB| = |DA| = 4 Trójkąt ABD (ale także trójkąt DCS) a=4 (|AD|) h=6 (|DB|)

	6*4
P=		=12
	2

(tu widac, że POLE równoległoboku jest RÓWNE 24 , allle pobawmy się dalej, bo zauwązyłem cóś dziwnego ...) |AB| = √|AD|²+|DB|² |AB| = √16+36 = √52 = 2√13 Trójkąt ASB (ale także trójkąt DSC) dzielimy go na dwa trójkąty (wysokośc) a=2√13 h=?

	|De|
h=		(z własności o odcinku łączącym środki dwóch boków)
	2

trójkąt DeB: Kąt eDB=60 stopni (nie chce mi się udowadniac ) więc |DB|=a√3 6=a√3

	6
a=
	√3

	6√3
a=		=2√3
	3

a w trójkącie eDB = 2*h w trójkącie ASB h=4√3 a=2√13 P=4√39 czyli pole równoległoboku = 8√39+12≠24 CZEMU? dla włąsnego bezpieczeństwa przepisz tylko do POLE RÓWNOLEGŁOBOKU JEST RÓWNE 24 dziękuję

R.W.16l: ale to jest chyba źle bo nie widzę potrzeby zaokrąglania ani w 1. ani w 2. przypadku

Bogdan: Dla dowolnego wypukłego czworokąta posiadającego przekątne d₁ i d₂ przecinające się pod

	1
kątem α, pole powierzchni P =		d1d2sinα.
	2

	1
W tym zadaniu: P =		* 10 * 6 * sin40o = 30 * 0,6428 ≈ 19,3
	2