aa ss: 4mod19 = 4mod11 jak to obliczyc formalnie?

ss: 4 + 19k = 4 mod 11 19k = 0 mod 11 19k = 209 mod 11 k = 19mod 11 4+19(19 + 11w) = 4+ 361+209w = 365 + 209w −> 365mod 209 = 156mod209 209−156= 53

henrys: Napisz treść zadania

Hugo: Jest to metoda Rabina, i dochodzimy tu do https://pl.wikipedia.org/wiki/Chi%C5%84skie_twierdzenie_o_resztach którego nie rozumiem. Chodzi o obliczenie tego równania modulo i innych. x = 4mod19 x = 4mod11 tu są równania http://scr.hu/2pdc/knrup

henrys: przed chwilą czytałem to w skrypcie

henrys:

Hugo: mi się wydaje ze ten układ nr2 spełnia to bo: 4mod11 = 4 + 11 = 15 15mod19 = 15 4 + 11k = 15mod19 11k =11mod19 k = 1mod19 = 1+19w 4+ 11k = 4+ 11(1+19w) = 4+11+209w = 15mod209 = 15? Co bys powiedział

Hugo: Hugo ma tu screena od pięknej znajomej http://scr.hu/2pdc/o9xz4 ale słabo rozumie. Ta dolna część sugerwałem się tą metodą. I tam oblicza x. x = 26 a potem tam nizej z nikąd odejmuje 133−26 =107 i zapisuje jako kolejne rozw 'x' . Jak sprawdzałem tam 107 nie pasuje do tamtych równań m.in 5mod7 bo: 5+7*14 = 103 a kolejne to 103+7 = 110 a jest zapisane x = 107 Co powiesz ?

henrys: powinna dodać 26+133

henrys: aaa, dobra jest ok

henrys: w tym układzie rozpatruje wszystkie 4 możliwości

Hugo:

Hugo: co ?! dlaczego? dlaczego 133 + 26 ? to jest posmolone , nie rozumiem tego czyli x₁ = 133 x₂ = 133+26 x₃ = 26 x₄ = 133−26 ? wszystkie wariacje 26 i 133?

Mila: x=4(mod19) x=4(mod 11) x−4 jest podzielne przez 11 i 19⇔ NWW(11,19}=209 x−4∊{209,418,627, ..}⇔ x∊{213,422,631,...}

Hugo: MIla

Mila:

Hugo: Milo proponujesz to tak rozwiązywać? właśnie w notatkach było że sprowadza się jedno równań do postaci a + b*k x=4(mod19) x=4(mod 11) 4 + 19k = 4mod11 następnie wyznaczało się k , podstawialo do rónania z x = 4+19k. Następnie tworzyło się ponownie modulo => stała mod 19(k) Twój sposób jest nie zwykle klarowny

Hugo: A tutaj? 4mod11 15mod19 Wdł Cb: x−4−15|209 ? Tam miałaś wcześniej dwie czwórki i połączyłaś. Wyciągnąć średnią artmeyczną z 4 i 15? emm Ale np liczba 15 mogla by to spełniać? 4 + 11 = 15 15 + 0 = 15

henrys: masz układ x=5mod7 x=7mod19 rozwiazanie x=26+133k drugi x=5mod7 x=12mod7 rowiązanie x=12 trzeci x=2mod7 x=7mod19 rozwiazanie x=121 czwarty x=2mod7 x=12mod19 rozwiązanie x=107] tyle

henrys: ucz się z notatek ładnych koleżanek bo dobrze notują

henrys: w drugi układzie drugie równanie powinno być x=12mod19

Hugo: szybka indukcja w między czasie Dla dowolnego naturalnego n na mocy indukcji. 2⁶ⁿ⁺⁷ + 3²ⁿ⁺² |11 n = 1... dla n+1 2⁶ⁿ⁺⁷ + 3²ⁿ⁺² = 11x 2⁶*2⁶ⁿ⁺⁷ + 3²*3²ⁿ⁺² = 64 * 2⁶ⁿ⁺⁷ + 9*3²ⁿ⁺² = 64(2⁶ⁿ⁺⁷ + 3²ⁿ⁺²) − 55* 3²ⁿ⁺² = 64* 11x − 11*5*3²ⁿ⁺² 11(64x − 5*3²ⁿ⁺²) Jest podzielne przez 11

Hugo: zaraz sb to przerobie czy mi tez tak wyjdzie

Hugo: jutro pisze o 12:30

Hugo: no powiedzmy ze to mam b) wyszło mi 12mod 49 i

Hugo: RSA umiem, indukcje umiem, z grafów mógłbym cos sie poradzic?

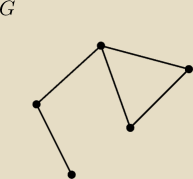
Hugo: Jest graf G, jak narysowac jego dopełnienie?

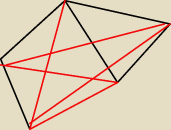
Hugo: to czerwone bz czarnego to jego dopełnienie?

Hugo: juz mam

Mila: Układ równań modulo ( dla różnych modułów) (1) x=4(mod11 )⇔ (1₁)x=11k+4 (2) x=15mod19 po podstawieniu do (2) 11k+4=15 (mod19) /−4 11k=11 (mod 19) /*7 77k=77( mod 19) (76k+k)=(76+1) (mod19) [76=4*19] k=1 (mod19)⇔k=19m+1 podstawiamy do (1₁) x=11*(19m+1)+4 x=209m+15 ============ Teraz możesz sprawdzić: m=1 x=15⇒15=11*1+4, 15=19*0+15 m=2 x=15+209=224, 224=19*11+15 ,224=11*19+15 itd

Mila: (3) Układ równań x=5 (mod7)⇔x=7k+5 x=7(mod19 ) =========== 7k+5=7 (mod 19) 7k=2 (mod 19) /*11 77k=22 (mod 19) 1k=3 (mod19)⇔[N[k=19m+3) x=7*(19m+3)+5 x=133m+21+5 x=26+133m, m∊C (?) x=26(mod133) ============

Hugo: Dziękuję , bardzo czytelnie !

Mila: Dobrze, że spojrzałeś− powodzenia.