rozwiąż nierówność Qwerty: witam, czy tego zadania nie można rozwiązać poprzez zastosowanie niewiadomej t? x⁴−5x²+4>0 x²=t t²−5t+4>0 delta = 1 t1=2 t2=3 x²=2 v x²=3 x1=−√2 v √2 x2=−√3 v √3 i zaznaczyć przedział

5-latek : Możesz tak policzyć ale delta zle policzona 25−16=?

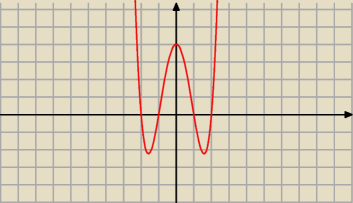
Janek191: Źle policzona Δ i dalej ....

Qwerty: ehh no tak, tak to jest jak się robi któreś tego typu zadanie i z pamięci delte wpisuje dziękuję za pokazanie błędu, muszę bardziej uważać przy tym

Qwerty: któreś z kolei tego typu zadanie*

5-latek : Możesz liczyc również tak (bez postawiania x⁴−5x+4 Δ= (−5)²−4*1*4=9 √9=3

	5−3
x12=		= 1 to x1= 1 lub x1= −1
	2

	5+3
x22=		=4 to x2= 2 lub x2=−2
	2

Qwerty: no tak, rzeczywiście tak będzie szybciej chyba dziękuję

5-latek : Rozwiaz sobie takich kilka przykladow żeby się z tym zapoznać A jeśli robisz podstawienie to zalozenie musisz zrobić zalozenie dla t≥0

5-latek : Przy tej metodzie co CI pokazałem to jeśli by wyszlo np. x₁²=−5 to tez nie ma rozwiązania

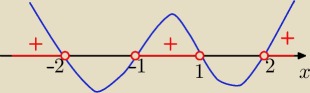
Eta: Można też tak: x⁴−x²−4x²+4= x²(x²−1)−4(x²−1)=(x²−1)(x²−4)=(x−1)(x+1)(x−2)(x+2) i rys. odp x∊ .......

Qwerty: ok teraz jadę kolejno zadania ze zbioru Kiełbasy, więc pewnie jeszcze się napotkam na takie zadania

5-latek: Można

Qwerty: Dziękuję Eta za ten pomysł, ale jednak jak jest możliwość to wolę tym łatwiejszym sposobem, bo niestety te grupowanie wyrazów na razie mi się jeszcze trochę myli, to znaczy "nie widzę" tego tak od razu chodzi mi o odejmowania, a później dodawanie, żeby ładnie było można pogrupować

Eta:

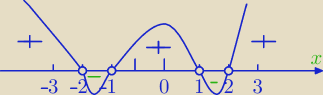
Mila: x⁴−5x²+4>0 x²=t, t≥0 t²−5t+4>0 Δ=25−16=9

	5−3		5+3
t1=		lub t2=
	2		2

t₁=1 lub t₂=4 (t−1)*(t−4)>0⇔ (x²−1)*(x²−4)>0⇔ (x−1)*(x+1)*(x−2)*(x+2)>0 Miejsca zerowe: −1,1,−2,2 odp. x∊(−∞,−2)∪(−1,1)∪(2,∞) =================

Eta: Mila czytaj wpis (rys. 18:07

Qwerty: dziekuje, dziekuje wszystkim zadanie już dawno zrobiłem i jadę kolejne