Wyznacz równanie okręgu. Rajmund: Wyznacz równanie okręgu o promieniu 4, stycznego do osi odciętych i prostej y=⁴₃x, którego środek leży w pierwszej ćwiartce układu współrzędnych. Oblicz pole wielokąta, którego wierzchołkami są: początek układu współrzędnych, środek okręgu i punkty styczności prostej z okręgiem.

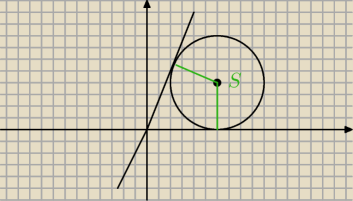
J: Srodek okręgu ma współrzedne: S(x,4) i jest odległy od prostej o 4 , współrzędną x ( dodatnią ) wyznaczasz ze wzoru na odległość prostej od punktu

Rajmund: "współrzędną x ( dodatnią ) wyznaczasz ze wzoru na odległość prostej od punktu" − to znaczy z tego: d=^|Ax0+By0+C_√A²+B²?

Rajmund: d=|Ax0+By0+C|/√A²+B²?*

J: tak .. i ta odległość jest równa promieniowi okręgu

5-latek : tak . A widzisz co to będzie za wielokąt ?

Rajmund: Nie wiem jak to wyznaczyć, czy chodzi o odległość punktu styczności okręgu z prostą OX od prostej x=0, czy o coś innego?

J:

	I−4x + 3*4 + 0I
4 =
	√32 + (−4)2

Rajmund: Aha, dobra, myślałem w ogóle o czymś innym. A co do drugiej części: w zadaniu jest "punkty styczności prostej z okręgiem", no ale przecież jest tylko jeden taki punkt, tak?

J: tak ... jeden punkt

Rajmund: Dziękuję.