Oblicz współrzędne wierzchołków tego trójkąta oraz wyznacz równanie okręgu... Jan: Bok AB trójkąta ABC zawiera się w prostej x+y−2=0, a bok AC − w prostej 3x−5y−14=0. Punkt S(0,−2) jest środkiem boku BC. Oblicz współrzędne wierzchołków tego trójkąta oraz wyznacz równanie okręgu opisanego na nim.

Eta:

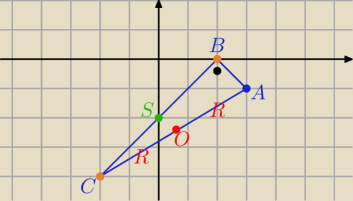
	⎧	x−y−2=0
1/ Rozwiąż układ równań:	⎩	3x−5y−14=0

otrzymasz A(3,−1)

	3		14		3		14
2/ B∊ y=−x+2 ⇒ B(xB, −xB+2) i C∊y=		x−		⇒ C(xC,		xC−		)
	5		5		5		5

D(0,−2) jest środkiem odcinka BC to x_B+x_C=0 ⇒ x_B= −x_C

	3		14
i yB+YC= −4 ⇒xB+		xC−		= −4 /*5
	5		5

to −5x_C+3x_C−14=−20 ⇒ ..... x_C= −2 to y_C= .... = −4 ⇒ C(−2,−4) x_B= 2 i y_B= .....=0 ⇒ B(2, 0) b) trójkąt ABC jest prostokątny bo

	yC−yB
wsp. kierunkowy aAB=−1 i aBC=		=...= 1
	xC−xB

zatem |∡ACB|=90^o to okrąg opisany na tym trójkącie ma środek O będący środkiem

	1
przeciwprostokątnej AC i R=		|AC|
	2

	xA+xC		yA+yC
zatem O(		,		)= ......=(................)
	2		2

	1
i R=		|AC|= ....
	2

o: (x−x_O)²+(y−y_O)²=R² ⇒ o: .................. dokończ............

Eta: Poprawiam chochlika ma być : " zatem |∡ABC|=90^o

teusz: Dzień dobry Eta, a dlaczego w pierwszym równaniu w układzie równań jest x−y−2=0?

Eta: To chochlik (sorry)

teusz: Każdemu zdarzają się błędy dziękuję za odp

Eta: To nie jest błąd ( to zwykły chochlik w zapisie

teusz: Rozkojarzenie przy wciskaniu klawisza

Eta: Dokładnie tym bardziej,że są obok siebie"+ i −"

Rajmund: Dziękuję

Eta: Jan podał zadanie , a Rajmund dziękuje

RJS: Gender

5-latek: Może ma Rajmund na drugie Ale ważne ze podziekowal