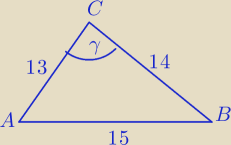
Oblicz wartość sinusa największego kąta w tym trójkącie. nacix: Boki trójkąta mają długości 13, 14 i 15. Oblicz wartość sinusa największego kąta w tym trójkącie.

6xdj: Najpierw sprawdz jaki to będzie trojkat a) prostokątny b) ostrokątny c) rozwartokątny

Metis: Skorzystałbym z tw. cosinusów , a potem z "jedynki". Ale nie wiem czy to najprostsze i poprawne rozwiązanie.

Janek191: p = 0,5 ( 13 + 14 + 15) = 21 p − a = 8 p − b = 7 p − c = 6 P_Δ = √21*8*7*6 = √7 056 = 84 oraz P_Δ = 0,5*13*14*sin α = 91 sin α = 84

	84
sin α =
	91

=============

Mila: Dobrze Metis . Rozwiąż.

Metis: Na podstawie twierdzenia cosinusów: 13²+14²−2*13*14*cosγ=15² 169+196−364cosγ=225 −364cosγ=−140 /:(−364)

	5
cosγ=
	13

Z "jedynki": sin² γ + cos² γ =1

	5
sin2 γ = 1− (		)2
	13

	144
sin2 γ =
	169

	144		12
sin γ = √		=
	169		13

RJS: W tym roku również piszę maturę R, więc rozwiążę skoro Metis nie podał rozwiązania.. 15²=13²+14²−2*13*14*cosγ 225=169+196−364cosy −109=−364cosγ / * (−1) 109=364cosγ

	109
cosy=
	364

Ok ?

Metis:

RJS: ?

Mila: RJS, masz pomyłkę w rachunkach, zamiast (−109) ma być inna liczba.

Janek191:

	140		35
cos γ =		=
	364		91

Metis: Janek na pewno dobrze?

Metis:

	5		35
...		=
	13		91

Mila: Dobrze.

35		7*5		5
	=		=
91		7*13		13

Janek191:

	35		5
Tak		=
	91		13

Moja uwaga była do RJS:

Eta:

	a2+b2−c2		169+196−225		140		5
cosγ=		=		=		=
	2ab		2*13*14		2*13*14		13

	12
sinγ=
	13