trójkąt równoramienny ABC Antek: Witam, zerknie jakaś dobra dusza na moje rozwiązanie Dany jest trójkąt równoramienny ABC, w którym AC BC = . Ponadto wiadomo, że A = −( ) 2,4 i B = − ( ) 6, 2 . Wierzchołek C należy do osi Oy. Oblicz współrzędne wierzchołka C. Obliczyłem środek odcinka AB: (2,1) wyznaczyłem wzór prostej AB, a w zasadzie tylko kierunkową a: −3/4=a a*a₂=−1<=> −3/4*a)₂=−1<=> a₂=4/3 prosta przechodząca przez środek odcinka AB i punkt C ma wzór: y=b, 1=2a+b 1=2*4/3+b b=−5/3 C=(0,5/3) ktoś sprawdzi, bardzo proszę o pomoc

J: najpierw napisz to zadanie porządnie

Antek: tzn?

Antek: A=( −2,4) B=( 6, −2)

J: Co oznacza: AC BC = Co oznacza: A = − ( ) 1,4 i B = − ( ) 6,2 ?

Antek: |AC|=|BC| nie zauważyłem tego błędu teraz już ok?

6xdj: A=(−2,4) B=(6,−2)

	−2−4		3
a=		=−		ok
	6−(−2))		4

	4
a1=
	3

y= a₁(x−x₀)+y₀ gdzie x₀=2 i y₀=1

	4
y=		(x−2)+1
	3

	4		5
y=		x−
	3		3

	5
C=(0,−		)
	3

Antek: Dzięki wielkie Dobrodzieju

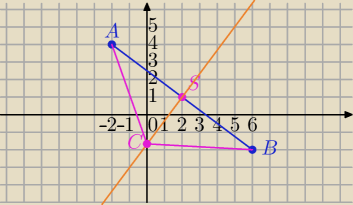
Mila: A=(−2,4) B=(6,−2) C=(0,y_c)

	−2+6		4−2
S=(		,		)=(2,1)
	2		2

AB^→[8,−6] Prosta AB:

x+2		y−4
	=		⇔
8		−6

	3		5
y=−		x+
	4		2

Prostopadła: m⊥AB i S∊m

	4
y=		x+b
	3

	4
1=		*2+b
	3

	8
b=1−
	3

	5
b=−
	3

	5
C=(0,−		)
	3

======