Kąt wpisany 6xdj: Mamy twierdzenie Jeżeli kąt wpisany jest oparty na polokregu to ten kąt jest prosty A gdyby okrag był bardzo wielki albo bardzo maly to może wcale ten kąt oparty na polokregu nie bylby prosty ? Jak to udowodnić ?

Janek191: Dowód jest dla dowolnego okręgu

J: twierdzenie o kącie środkowym i wpisanym opartych na tym samym łuku okręgu

6xdj: Tak ja znam to twierdzenie . Jest to zadanie z klasy 5 . mam przeprowadzić dowod wiedzac ze dwusieczna kąta jest jego osia symetrii i suma kątow czworokąta jest rowna 360 stopni

Mila: Może zapisz precyzyjnie treść zadania.

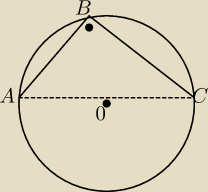
6xdj: problem jest taki Podane to twierdzenie i czy zawsze będzie to kat prosty? Watpliwosc a jeśli będzie to bardzo duzy lub bardzo maly okrag ? Na kilku rysunkach to możemy sprawdzić ale przecież nie sprawdzimy wszystkich przypadkow Żeby mieć calkowita pewność musimy to udowowdnic

:): w matematyce nieważna jest wielkość (przynajmniej nie tu)

6xdj:

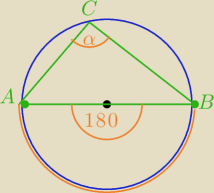
Mila: Jeżeli kąt wpisany jest oparty na półokregu to ten kąt jest prosty . Wcześniej na pewno udowodniono tw. o kacie wpisanym i środkowym opartych na tym samym łuku. Miara kąta wpisanego jest dwa razy mniejsza od miary kąta środkowego opartego na tym samym łuku.

	1
α=		*180o⇔
	2

α=90^o

PW: Dowód tego twierdzenia jest bardzo prosty, ale sugestia podana o 19:00 nijak się ma do tego znanego dowodu. Potrzebna jest wiedza, że trójkąt równoramienny ma równe kąty między ramionami a podstawą oraz że suma kątów trójkąta jest równa 180° (tylko nie pytaj, czy dla bardzo dużych trójkątów też tyle wynosi).

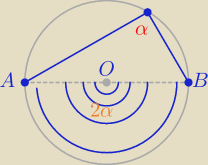
Eta: 2α=180^o −− miara kąta środkowego ( niezależnie od wielkości okręgu ! to α= 90^o Ejjj "małolatku" ... czemu się ukrywasz

6xdj:

Eta:

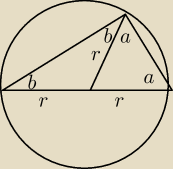
PW: a+a+b+b = 180°, a więc a+b=90°

Eta: Też ładnie

Eta: Jeszcze ładniej by było α+α+β+β=180^o

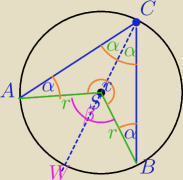
Mila: Półprosta CS− dwusieczna kąta ACB ΔASC,ΔBSC−− trójkąty równoramienne x+2α+2α=360 4α=360^o−x 4α=β− kąt środkowy oparty na łuku AWB

	1
2α=		β ⇔
	2

Miara kąta wpisanego ACB jest dwa razy mniejsza od miary kąta środkowego opartego na tym samym łuku. ==============================

PW: Rysowanie tak mnie irytuje, że już nie ryzykowałem, czy "wskoczą" greckie litery. A z tego samego rysunku wywodzi się, że β jest połową kąta środkowego opartego na tym samym łuku. Jest to szczególny przypadek twierdzenia o kącie wpisanym i środkowym, po pewnym zastanowieniu można z niego wyprowadzić dowód ogólny.

PW: O, po obejrzeniu rysunku Mili widać czego dotyczyła sugestia z 19:00

6xdj: Dziekuje wszystkim Mogloby się wydawac to irytujące bo to przecież oczywiste , ale wcale nie było to takie proste

6xdj: I przepraszam to nie klasa 5 tylko klasa 7

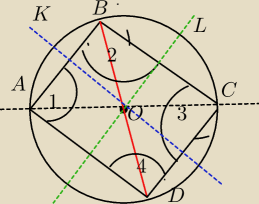
4max: A moze tak ? Troche ten rysunek mi nie wyszedl na rysunku z 23;18 dorysować srednice BD i cięciwy AD i CD Dostaniesz czworokąt ABCD . Dwusieczna OK kata AOB jest osia symetrii otrzymanej figury Kat 1 jest symetryczny względem OK do kata 2 a kat nr 4 do kata nr 3 Dlatego kat nr 1 =kat nr 2 a kat nr 4 = kat nr 3 Druga osia symetrii jest dwusieczna OL kata srodkowego BOC Kat nr 2 jest symetryczny względem OL do kata nr 3 wiec kat nr 2= kat nr 3 wiec kat nr 1=kat nr 2 = kat nr 3 = kat nr 4 czyli wszystkie katy sa rowne Ponieważ suma ka tow w czworokącie wynosi 360 stopni to każdy z tych katow wynosi 360:4=90 stopni Wiec kat ABC jest prosty

PW: Cytat: Dostaniesz czworokąt ABCD . Dwusieczna OK kata AOB jest osia symetrii otrzymanej figury. Pytanie: – A wynika to z głębokiego przekonania? Czy można to udowodnić, ale dowód jest trudniejszy niż dowód rozpatrywanego problemu?