Oblicz współrzędne wierzchołków trójkąta. Jan: Trójkąt równoramienny jest wpisany w okrąg (x−1)²+(y−2)²=50. Oblicz współrzędne wierzchołków trójkąta, wiedząc, że: a) podstawa trójkąta jest zawarta w prostej y=x−7, b) jedno z ramion trójkąta jest zawarte w prostej y=¹₂x+4.

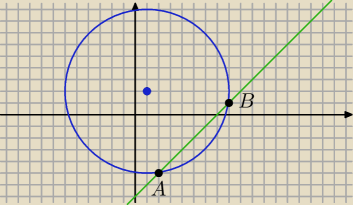
6xdj: a) zielona to y=x−7 Do równania okręgu wstaw za y=x−7 i wylicz punkty przeciecia prostej z okręgiem Powrot do przeszlosci i przypominamy sobie pod jakim katem pada wysokość w tojkącie na podstawe i w jakim punkcie pada wysokość na podstawe w trojkacie równoramiennym Jeśli to już wiemy to liczmy srodek odcinka AB i piszsemy równanie prostej prostopadlej do AB i przechodzącej przez srodek odcinka AB Liczymy teraz punkty przecięcia tej prostej prostopadlej i okręgu .

Janek191: Wystarczy podać równanie prostej prostopadłej do danej i przechodzącej przez S = (1; 2).

Jan: Ok, a jak podpunkt B? Układ równań z prostą i kołem, a z tego wychodzi mi x∊{−6;6}, co dalej?

4max: Ja chodzde do gimnazjum ale wydaje mi się ze jeśli masz układ dwóch rownan i dwie niewiadone to musisz je wyznaczyć

Jan: Tak zrobiłem, wyszły mi punkty: A(−6;1) i B(6;7), tylko teraz nie wiem co dalej.

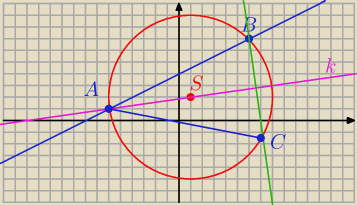
Janek191: b) ( x −1)² + ( y −2)² = 50 S = ( 1; 2) r = 5√2 y = 0,5 x + 4 Wyznaczamy punkty wspólne prostej i okręgu: x² − 2x + 1 + ( 0,5 x +2)² = 50 x² − 2 x + 1 + 0,25 x² + 2 x + 4 = 50 1,25 x² = 45 x² = 36 x = − 6 lub x = 6 więc y = 0,5*(−6) + 4 = 1 lub y = 0,5*6 + 4 = 7 A = (− 6; 1) B = ( 6; 7) ==================== S = ( 1; 2) Prosta AS y = a x + b 1 = − 6a + b 2 = a + b −−−−−−−−−−−−

	1
1 = 7 a ⇒ a =
	7

	1		13
b = 2 −		=
	7		7

	1		13
k : y =		x +
	7		7

==================== Przez punkt B prowadzimy prostą prostopadłą do k : y = − 7 x + p 7 = − 7*6 + p ⇒ p = 49 y = − 7 x + 49 ========== Szukam punktu wspólnego tej prostej oraz okręgu: x² − 2 x + 1 + ( − 7 x + 47)² = 50 x² − 2 x + 1 + 49 x² − 658 x + 2209 = 50 50 x² − 660 x + 2160 = 0 / : 10 5 x² − 66x + 216 = 0 Δ = 4356 − 4320 = 36 √Δ = 6

	66 − 6		72
x =		= 6 lub x =		= 7,2
	10		10

y = − 7*7,2 + 49 = −1,4 C = ( 7,2; −1,4) =========== Jest jeszcze drugie rozwiązanie ( wtedy BA = BC )

Jan: Dzięki