Rozwiąż równanie x^2+|x-1|=0
dsa: Rozwiąż równianie
x2+|x−1|=0
Rozbijamy na dwa przypadki?
kiedy x>0 x<=0 ?
28 sie 18:40
Bogdan:
dwa przypadki: dla x < 1 oraz dla x ≥ 1 (tu są znaki ≤ i ≥)
28 sie 18:51
ICSP: x2 ≥ 0
|x − 1| ≥ 0
x2 + |x − 1| ≥ 0
ale równość nie zajdzie poniważ x2 orwaz |x−1| jednocześnie się nie zerują. Równanie
sprzeczne.
28 sie 19:00
ZKS:
x2 + |x − 1| = 0
x2 = −|x − 1|
Lewa strona jest nieujemna natomiast prawa niedodatnia, zatem jedynym możliwym rozwiązaniem
będzie, kiedy x2 = 0 ∧ −|x − 1| = 0, ale jak łatwo zauważyć taka sytuacja nie zajdzie, zatem
otrzymujemy brak rozwiązań.
28 sie 19:00
Eta:
x
2= −|x−1|
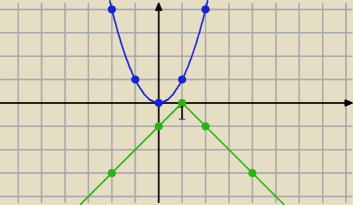
f(x)=x
2 ,
g(x)=−|x−1|
wykresy nie mają punktów wspólnych
zatem równanie nie ma rozwiązań
28 sie 19:09
 x2= −|x−1|
f(x)=x2 , g(x)=−|x−1|
wykresy nie mają punktów wspólnych
zatem równanie nie ma rozwiązań
x2= −|x−1|
f(x)=x2 , g(x)=−|x−1|
wykresy nie mają punktów wspólnych
zatem równanie nie ma rozwiązań