geometria Asmander: wykaż , że jeśli bok ośmiokąta foremnego ma długość a, to promień okręgu opisanego na tym

	a
ośmiokącie jest równy		√4+√8
	2

henrys: z twierdzenia cosinusów

Janek191:

	0,5 a
sin 22,5o =		/ * 2 r
	r

2 r*sin 22,5^o = a

	a		a
r =		=		=
	2 sin 22,5o		√2 −√2   2 *   2

	a		√2 +√2		a*(√2 +√2)		√2
=		*		=		*		=
	√2 − √2		√2 + √2		√2		√2

	a		a
=		*√4 + 2√2 =		*√4 + √8
	2		2

henrys: miara kata środkowego jest równa 45^o, czyli a²=2r²−2r²cos45^o a²=r²(2−√2)

	a2
r2=
	2−√2

	a		a√2−√2		a√2−√2(2+√2)		a
r=		=		=		=		√2(2+√2)
	√2−√2		2−√2		2		2

	a
r=		√4+√8
	2

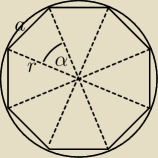Rybson: α=^360°₈=45° r−promień okręgu opisanego na tym ośmiokącie Korzystam z tw. cosinusów: a²=r²+r²−2*r*r*cos45°

	√2
a2=2r2−2r2*
	2

a²=2r²−√2r²

	a2
r2=
	2−√2

	a2(2+√2)
r2=
	4−2

	a2(2+√2)
r=√
	2

...

	a
,stąd r=		√4+√8
	2

c.n.w

Asmander: Dziękuję wszystkim za rozwiązania

Asmander: Dziękuję wszystkim za rozwiązania