Znajdź równania prostych równoległych do prostej. Leo: Znajdź równania prostych równoległych do prostej x−y+6=0, wyznaczających w przecięciu z kołem x²+y²≤20 cięciwy długości 6√2.

prosta: można wyznaczyć odległość cięciwy od środka koła i liczyć dalej korzystając ze wzoru na odległość punktu od prostej

Leo: A jak znaleźć punkt na cięciwie skoro nie wiem, gdzie są te proste równoległe?

prosta: punktu nie potrzebujemy. r=2√5 l=6√2 d− odległość cięciwy od środka okręgu Z tw .Pitagorasa: d²+(3√2)²=(√5)² d²=25−18 d=√7

.: jakie to proste

prosta: każda prosta równoległa do prostej x−y+6=0 opisana jest równaniem: x−y+C=0 jej odległość od środka koła jest równa:

	|C|		|Ax+By+C|
d=		na podstawie wzoru d=
	√12+(−1)2		√A2+B2

	|C|
stąd		=√7, |C| =√14
	√2

Leo: Powinno być: Z tw. Pitagorasa: d²+(3√2)²=(2√5)². Dziękuję.

prosta: racja

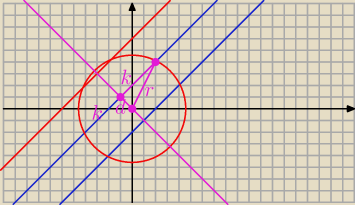
Janek191: x² + y² ≤ 20 ⇒ r² = 4*5 r = 2√5 −−−−−−k oraz 2 k = 6 √2 k = 3 √2 −−−−−−− Mamy r² = d² + k² d² = 20 − (3√2)² = 20 − 18 = 2 d = √2 Prosta równoległa do prostej x − y + 6 = 0 ma postać x − y + C = 0 a odległość tej prostej od środka koła S = (0, 0) jest równa d = √2, zatem mamy

	I 1*0 − 1*0 + C I
d =		= √2
	√12 +(−1)2

I C I
	= √2
√2

I C I = 2 C = − 2 lub C = 2 Szukane proste równoległe do danej prostej mają równania: x − y − 2 = 0 oraz x − y + 2 = 0 ========= ===========