Pomocy :)) Krzyś: Dla jakich wartości parametru a równanie |x−2|=a²−3a−2 ma dwa pierwiastki różnych znaków?

:): po pierwsze a²−3a−2> 0, ale czy to wystarczy...

:): jakby było |x| to by to wystarczyło a tu mamy przesunięcie co nie..

Krzyś: może jeszcze : −a²+3a+2<0 ?

:): Nie no skad.. z definicji |cokolwiek| ≥0..... (przypadek =0 odrzuciliśmy bo wtedy by było 1 rozwiązanie)

:): a²−3a−2>0 (to "max") chodzi o to, że jeszcze nie wszystkie takie a i tak są dobre

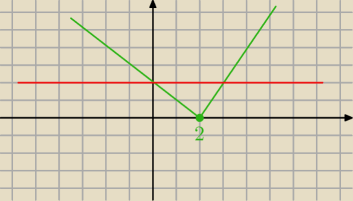
J: czerwona linia: y = a² − 3a − 2

Krzyś: To jakie jeszcze założenia trzeba zrobić?

J: trochę przestrzeliłem wykres : y = I x − 2 I ( zielony )

:): zuważ że jakby np byo |x−2|=1 to x=1 i x=2 jest dobry... czyli nie wszystkie dodatnie.....

:): i x=3***

J: czerwona linia musi leżeć powyżej: y = 2

PW: Po prostu najpierw rozstrzygnąć, dla jakich p >0 równanie |x−2| = p ma rozwiązania różnych znaków.

:): ; )

J: a² − 3a − 2 > 2

:): Nie jesteśmy chyba dobrymi dydaktykami

Krzyś: Dzięki

ZKS: Tak jak PW pisze. Równanie |x − 2| = p ma dwa pierwiastki dla p > 0, teraz rozpisujemy dalej x − 2 = p ∨ x − 2 = −p x = p + 2 ∨ x = 2 − p skoro p > 0 oraz mamy mieć różnych znaków pierwiastki to liczba 2 − p musi być ujemna, ponieważ p + 2 jest zawsze dodatnie dla p > 0, zatem warunki jakie musimy dać to a² − 3a − 2 > 0 [dwa pierwiastki] 2 − a² + 3a + 2 < 0 [dwa różne pierwiastki].

J: nie kijem go, tylko pałą

:): Myśle, że jak on to zobaczy..to zniszczyłeś mój nadzieje, że coś z tego rozumie

:): mu jego***