 Może tak :
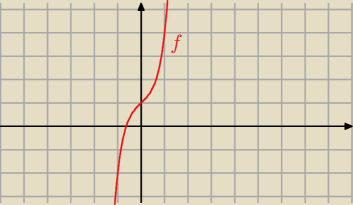
Jeżeli funkcja y = f(x) jest silnie monotoniczna i różniczkowalna w pewnym zbiorze X oraz
f '(x) ≠ 0 dla x ∊ X, to funkcja odwrotna x = f−1 ( y) jest różniczkowalna na zbiorze Y
wartości funkcji f, przy czym
Może tak :
Jeżeli funkcja y = f(x) jest silnie monotoniczna i różniczkowalna w pewnym zbiorze X oraz
f '(x) ≠ 0 dla x ∊ X, to funkcja odwrotna x = f−1 ( y) jest różniczkowalna na zbiorze Y
wartości funkcji f, przy czym
| 1 | ||
[ f−1(y)] ' = | . | |
| f '(x) |
| 1 | 1 | |||
[ f−1 (1)] ' = | = | = 1 | ||
| f '(0) | 1 |