prosze o pomoc mila166: Miara kąta ostrego równa się α i 4 sinα=p {5} cosα a). Oblicz wartość wyrażenia tg²α−21/16 sinα b). Sprawdz czy α > 30º

:): przepisz jeszcze raz początek..bo cos tam nie widać

mila16: Miara kąta ostrego rowna się α i 4 sin α = √5 cos α. Oblicz wartość wyrażenia tg² α − 21/16 sin α

:): 4sinα=√5cosα czyli ^sinα_cosα = ^√5₄, tg=sin/cos............

mila16: Wiem tylko mi bardzo dziwny wynik wychodzi i chcialabym zeby ktos to obliczył

:): najważniejsze, że wiesz jak policzyć. Wynik jest drugorzędny

pigor: ..., np. tak: a) −−−−−−−−−−−−−−−−−−−−− 4sinα= √5cosα /² i sin²α+cos²α= 1 /*5 ⇒ ⇒ 16sin²α−5cos²α=0 i 5sin²α+5cos²α= 5 /+stronami ⇒ ⇒ 21sin²α=5 i 5cos²α= 5−²⁵₂₁ ⇒ sin²α= ⁵₂₁ i cos²α= 1−⁵₂₁ ⇒

	√5		5
⇒ sinα=		i tg2α=		⇒
	√21		16

	21		5		21		√5		5		√105
⇒ tg2α−		sinα=		−		*		=		−		=
	16		16		16		√21		16		16

= ¹₁₆(5 − √105) < 0 , b) −−−−−−−−−−−−−−−−−−−−−−−−−− gdyby było α >30^o ⇒ sinα > sin30^o= ¹₂ no to zobaczmy ; tu mamy sinα=√⁵₂₁ , a więc 21 >20 ⇒ ¹₂₁< ¹₂₀ ⇔ ⁵₂₁< ⁵₂₀= ¹₄ ⇒ ⇒ √⁵₂₁=sinα < ¹₂= sin30^o ⇒ α < 30^o , a więc NIE. ...

mila16: Ok bardzo dziękuję za pomoc

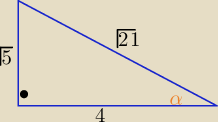
Eta: α−− kąt ostry

	√5		5		√5		√105
4sinα= √5cosα ⇒ tgα=		to tg2α=		i sinα=		=
	4		16		√21		21

	5		21		√105		1
W=		−		*		=		(5−√105)
	16		16		21		16