prosze o pomoc
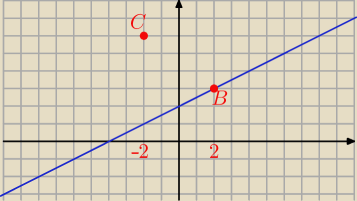
mila16: Punkty B=(2, 3) i C=(−2, 6) sa wierzcholkami trójkąta ABC. Osią symetrii tego trójkąta jest
prosta x−2y+4=0. Wyznacz współrzędne punktu A
24 sie 20:53
:): geometria−−> nie wiem co robić, zaczynam od rysunku!

24 sie 20:54
mila16: A co dalej?
24 sie 21:33
J:
na początek wyznacz środek odcinka BC
24 sie 21:43
Mila:
Dobrze zapisałaś współrzędne?
24 sie 21:48
J:
a jeśli należy do tej prostej, to tych trójkątów jest nieskończenie wiele
24 sie 21:49
mila16: Takie mam zadanie i raczej jeden trojkat powinien powstac
24 sie 21:53
Janek191:
24 sie 21:56
Janek191:
A będzie symetryczny do C względem danej prostej.
24 sie 21:57
Janek191:
1) Wyznacz prostą prostopadłą do danej prostej przechodzącą przez C
2) Wyznacz punkt wspólny tych prostych, który będzie środkiem odcinka AC
3) Wyznacz punkt A
24 sie 22:00
Mila:
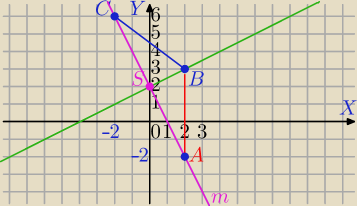
C=(−2,6)
m⊥k i C∊m
m: y=−2x+b
6=−2*(−2)+b⇔b=2
m: y=−2x+2
S(0,2) punkt przecięcia prostych
S jest środkiem odcinka CA
y
a=−2
A=(2,−2)
24 sie 22:00
pigor: ..., wierzchołek B=(2,3) leży na danej prostej, więc
| | x+2 | | y−6 | |
równanie prostej AC, to np. |
| = |
| ⇔ −2x−4= y−6 , więc |
| | 1 | | −2 | |
środek AC, to punkt S=(x,y) taki, że y= −2x+2 i x+4x−4+4=0 ⇔
⇔ (x,y)=
S=(0,2), zatem jeśli
C=(−2,6) i
A=(x,y)=? ⇒
⇒ x−2= 0 i y+6=2 ⇔
A=(2,−4) −szukany wierzchołek . ...

24 sie 22:04
pigor: ..., przepraszam , oczywiście powinno być u mnie
w ostatniej linijce y+6=
4, wtedy y= −2 i
A=(2,−2)...

24 sie 22:08
mila16: Bardzo dziękuję za pomoc

24 sie 23:39


 C=(−2,6)
C=(−2,6)


