Pole powierzchni Całka oznaczona po dy matrix: Cześć, mam problem z zadaniem: Oblicz pole figury ograniczonej krzywymi : y² = 2x − 2 oraz y=2x−14 Narysowałem rysunek do tego i wychodzi, że muszę sobie odwrócić rysunek i zmienić granice całkowania na y i wtedy liczyc. Rysunek: http://fotowrzut.pl/XJIA4BQESM Pytanie 1: Czy jeśli zamieniam granice całkowania i ten rysunek to całą funkcję muszę zamienić na x(y) zeby całke liczyć po dy ? Jeśli tak to wyszlo mi : x= (y² +2) / 2 i x= (y+14)/2 Tyle, że przy liczeniu całki oznaczonej jeśli biorę 2 oddzielne całki jedna w granicach <−3,0> druga <0,4 > (−3 i 4 to punkty przeciecia tych prostych wedlug moich obliczeń) to wynik wychodzi 8/3 a jeśli liczę to jako jedną całkę w granicach <−3, 4> to wynik wychodzi ujemny czyli sprzeczność. Pomoże ktoś co robię źle? Z góry dzięki za pomoc

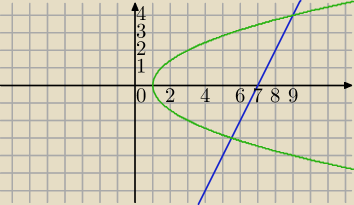
Mila: Oblicz pole figury ograniczonej krzywymi : y² = 2x − 2 oraz y=2x−14 y²=2x−2 y=2x−14 Granice:

	1
2x=y+14⇔x=		y+7
	2

y²=y+14−2 y²−y−12=0 Δ=1+48=49

	1−7		1+7
y=		=−3 lub y=		=4
	2		2

============================

	1		1		1		1
P=−3∫4(		y+7−		y2−1) dy=−3∫4(		y−		y2+6) dy
	2		2		2		2

	1		1
=[		y2−		y3+6y]−34=
	4		6

1		1		1		1
	*16−		*64+6*4−(		*9+		*27−18)=
4		6		4		6

	7
=28
	12

matrix: a skąd wiadomo, że wykres trzeba obrócić w lewo (wtedy zielona bedzie na dole) a nie w prawo?

Mila: Nie rozumiem, o co pytasz, czy masz problem z narysowaniem paraboli?

matrix: chodzi mi o to, skąd wiesz, która funkcja jest na górze a która na dole? bo jakby odwrócić układ w drugą stronę, to wtedy będzie odwrotnie

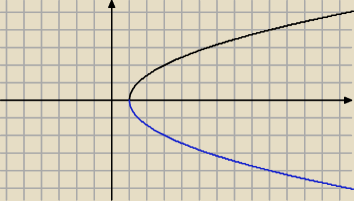
5-latek: Mnie się wydaje ze student nie powinien mieć problemu z narysowaniem funkcji y²=2x−2 przecież y= √2x−2 (czarna ) a także y=−√2x−2 niebieska

prosta: jak odwrócisz układ w drugą stronę i prawidłowo narysujesz wykresy to będzie tak samo

matrix: juz nic, dzieki

Mila:

Mila: Witaj 5−latek.

5-latek: Witaj Milu Pozdrawiam .