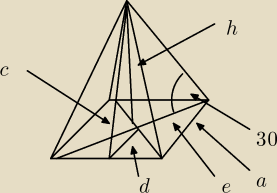
 wysokość wynosi h=√6 zadany jest kąt α=30o
tg 30 = h/e gdzie e to połowa przekątnej podstawy
zatem e=h/(tg 30)
bok a ma długość a=e √2 (trójkąt prostokątny równoramienny)
czyli a=√2 * √6 / (tg 30)
a= √2 * √6 * √3 =6
możemy teraz obliczyć objętość v=1/3 * a2 *h = (1/3)*36* √6 = 12 √6
wysokość ścianki bocznej wyznaczamy z tw Pitagorasa (d=a/2):
c2 = (a/2)2 +h2
c2= 32 + 6
c= √15
pole powerzchni bocznej to:
p=4*(c*a/2) + a2
p= 2*c*a + a2
p= 2 * √15 * 6 + 36
p = 12 √15 +36
wysokość wynosi h=√6 zadany jest kąt α=30o
tg 30 = h/e gdzie e to połowa przekątnej podstawy
zatem e=h/(tg 30)
bok a ma długość a=e √2 (trójkąt prostokątny równoramienny)
czyli a=√2 * √6 / (tg 30)
a= √2 * √6 * √3 =6
możemy teraz obliczyć objętość v=1/3 * a2 *h = (1/3)*36* √6 = 12 √6
wysokość ścianki bocznej wyznaczamy z tw Pitagorasa (d=a/2):
c2 = (a/2)2 +h2
c2= 32 + 6
c= √15
pole powerzchni bocznej to:
p=4*(c*a/2) + a2
p= 2*c*a + a2
p= 2 * √15 * 6 + 36
p = 12 √15 +36
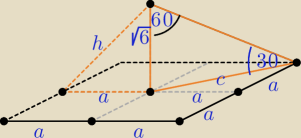 A co to za niestaranny ksstach rysunek, linie niedociagnięte, oznaczenia niejasne,
niewłasciwy format linii.
Na podstawie własności trójkata prostokątnego o kącie ostrym o mierze 30o:
c = √6*√3 = 3√2
A co to za niestaranny ksstach rysunek, linie niedociagnięte, oznaczenia niejasne,
niewłasciwy format linii.
Na podstawie własności trójkata prostokątnego o kącie ostrym o mierze 30o:
c = √6*√3 = 3√2
| 1 | 1 | |||
Objętość ostrosłupa V = | * | (2c)2*√6 = 12√6 | ||
| 3 | 2 |