matura Eta: matura 2 czerwca 2015 Kto chętny? http://jakzdacmaturezmatematyki.pl/files/matury/matura_matematyka_2015-06-02_PR_SM.pdf

Eta: Zaklepuję zad4

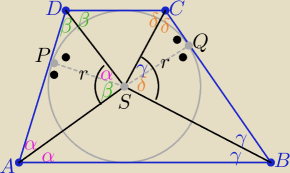Eta: 2α+2β=180^o ⇒ α+β=90^o i analogicznie : γ+δ=90^o dokładny komentarz pozostawiam (dla przyszłych maturzystów r²=|AP|*|DP| i r²= |BQ|*|CQ| ( dlaczego? i stąd .... mamy tezę do tego dokładny komentarz i już mamy 3pkt

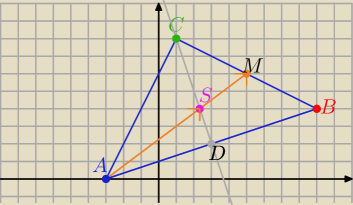Eta: Bardzo ładne zad. 8 6pkt AM jest środkową trójkta Środkowe dzielą się w stosunku 2:1 licząc od wierzchołka Punkt S przecięcia środkowych −−− jest środkiem ciężkości trójkąta to → → AS=2SM ⇒[x+3, y]=2[5−x,6−y] ⇒ .... x=⁷₃ i y=4 to S(⁷₃, 4) proste CS⊥AB ⇒ CS: y=−3(x−⁷₃)+4 ⇒ CS: y=−3x+11 CS∩AB={D} −− środek podstawy AB

	1
rozwiązując układ równań: y= −		x+1 i y= −3x+11 ⇒ D(3,2)
	3

stąd x_B=2x_D−x_A i y_B=2yD−yA ⇒ .... B(9,4) Można jeszcze wyznaczyć współrzędne punktu C korzystając ,że S jest środkiem ciężkości tego trójkąta

	xA+xB+xC		yA+yB+yC
		=xS i		=yS
	3		3

stąd x_C= 1 i y_C= 8 to C(1,8) Do tego narysować trójkąt w układzie współrzędnych(i podać dokładne komentarze ) i mamy 6pkt

Szachista : Może pani zrobić 1 bo próbowałem ją zrobić ale coś nie tak robię .

ZKS: x² + 2(m − 1)x + m² + m − 1 = 0 x² + 2(m − 1)x + (m − 1)² + 3m − 2 = 0 (x + m − 1)² = 2 − 3m

	2
Mamy mieć dwa różne pierwiastki zatem 2 − 3m > 0 ⇒ m <		.
	3

(x₁ + x₂)(x₁² + x₂²) = x₁³ + x₂³ + x₁x₂(x₁ + x₂) < x₁³ + x₂³ x₁x₂(x₁ + x₂) < 0 (m² + m − 1)[−2(m − 1)] < 0

	1		5
(m2 + m +		−		)(m − 1) > 0
	4		4

	1		5
[(m +		)2 −		](m − 1) > 0
	2		4

	1 − √5		1 + √5
(m +		)(m +		)(m − 1) > 0
	2		2

	−1 − √5		−1 + √5
m ∊ (		;		) ∪ (1 ; ∞)
	2		2

	−1 − √5		−1 + √5		2
m ∊ (		;		) ∪ (1 ; ∞) ∩ m ∊ (−∞ ;		)
	2		2		3

	−1 − √5		−1 + √5
m ∊ (		;		).
	2		2

Eta: Zamiast tego "myku"

	2
Δ>0 ⇒ ...... m<
	3