Rozwiąż równanie w zbiorze liczb zespolonych: (Z^4)+i(Z^3)+2=0 Kaprikos: Rozwiąż równanie w zbiorze liczb zespolonych: Z⁴+i(Z³)+2=0 Bardzo proszę o pomoc.

5-latek: czepiam się ale co to jest Z⁴ ?

Kaprikos: Z to oznaczenie liczby zespolonej, a 4 to potęga.

5-latek: Ale oznaczenie liczby zespolonej jest takie z=a+ib

ICSP: a,b ∊ R W równaniach przyjmuje się oznaczenie z.

Kaprikos: No to sam sobie odpowiedziałeś na pytanie czym jest Z.

Mila: To jest równanie ze zbioru? Może tam jest : z⁴+i*z²+2=0 ?

5-latek: Dzien dobry Milu Pozdrawiam

Kaprikos: Ogólnie mam 2 równania jedno właśnie to co Ty napisałeś: z⁴+i(z²)+2=0 a drugie to co ja napisałem: z⁴+i(z³)+2=0, ale postanowiłem dodać to trudniejsze. Jeżeli umiesz rozwiązać to gdzie jest z² to również bardzo proszę.

5-latek: ja jeszcze nie umiem tego rozwiazywac ale przy tym równaniu z⁴+iz²+2=0 można zrobić podstawienie z²=t t²+it+2=0 Teraz delta =i²−8 = −1−8= −9 √−9= i√9 (ale nie weim czy dobrze

Janek191: √−9 = √ 9 i² = 3 i lub √−9 = − 3 i

5-latek: Janek A możesz dalej to rozwiazac ?

Asia: Janek191 ale to chyba nie jest rozwiazane w ukladzie liczb zespolonych

5-latek:

	−i−3i
t1=
	2

	−i+3i
t2=
	2

	−i−(−3i)		−i+3i
t3=		=
	2		2

	−i−3i
t4=
	2

czyli t₃ i t₄ wyszly takie same jak t₂ i t₁ Ale jak wrocic do podstawienia ?

Janek191:

	− i − 3i		− i +3 i
t =		= − 2 i lub t =		= i
	2		2

czyli z² = − 2i lub z² = i z² = ( 1 − i)² z = 1 − i lub z = − 1 + i itd. z² = i = 0 + i = cos0,5π + i sin 0,5π itd

Janek191: z² = cos 0,5π + i sin 0,5π i teraz wzór na pierwiastek n −tego stopnia z liczby zespolonej

5-latek: dziekuje .

ICSP:

	1		1
i =		* 2i =		(1 + i)2
	2		2

Mila: z⁴+i*z²+2=0 z²=t t²+it+2=0 Δ=i²−4*2=−9

	−i−3i		−i+3i
t1=		=−2i lub t2=		=i
	2		2

z²=−2i lub z²=i z=√−2i lub z=√i Dalej obliczysz, czy potrzebna pomoc? albo rozwiązujesz układy równań, albo wzory de Moivre'a

	√2		√2		√2		√2
1−i, −1+i,		+i*		, −		−i*
	2		2		2		2

Janek191: Czyli dodatkowo

	1		1
z =		(1 + i) lub z = −		( 1 + i)
	√2		√2

Kaprikos: Dzięki chłopaki za rozwiązania

Janek191: I ma całe zadanie ( jedno )

Benny: Ja doszedłem do takiego rozkładu. z⁴+iz³+2=0 [z²+z(i−1)−(i−1)][z²+z(i+1)+i+1]=0

ICSP: Benny twój rozkłąd dotyczy wielomianu : z⁴ + 2iz + 2

ICSP: 2iz³ *

henrys: cześć no niestety http://www.wolframalpha.com/input/?i=z%5E4%2Biz%5E3%2B2%3D0

Benny: To coś musiałem zgubić

Benny: No na początku samym błąd był. Napisałem, że (z²+iz)²=z⁴+iz³+i²z²

Kaprikos: Mila, a mogłabyś napisać jak doszłaś do tych wyników? Ja za cholerę nie mogę

Mila: Czy masz odpowiedź do równania: z⁴+i*z³+2=0 ?

Kaprikos: Niestety nie mam do nich odpowiedzi, ale chodziło mi o przykład z⁴+i*z²+2=0, który robiłaś i o wyniki po pierwiastkowaniu, które napisałaś, skąd one się wzięły, bo ani moivrem ani w inny sposób nie chcą mi wyjść,

Mila: Za chwilę napiszę.

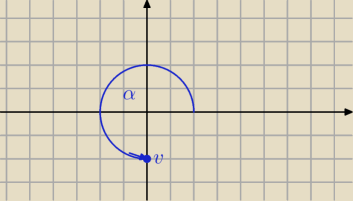
Mila: z=√−2i liczba v=(−2i) to na płaszczyźnie zespolonej punkt (0,−2)

	3π
α=		− argument liczby (−2i)
	2

|v|=2

	3π		3π		3π		3π
z0=√2*(cos		+i sin		=2*(cos		+i sin
	2*2		2*2		4		4

	√2		√2
z0=√2*(−		+i		)=−1+i
	2		2

	3π   +2π 2		3π   +2π 2
z1=√2*(cos		+isin		)
	2		2

	7π		7π		√2		√2
z1=√2*(cos		+i sin		)=√2*(		−i		)
	4		4		2		2

z₁=(1−i) ============= Albo tak: √−2i=x+iy, x,y∊R⇔ −2i=(x+iy)² −2i=x²−y²+2xyi⇔ x²−y²=0 i 2xy=−2

	1
y=−
	x

	1
x2−		=0
	x2

x⁴−1=0 x=1 lub x=−1 y=−1 lub y=1 z=1−i lub z=−1+i Czy zrobisz √i sam? Czy napisać?